Archivo de la etiqueta: números enteros

CONSTELACIONES NUMERICAS
Los esquemas ya no son lo que eran. Uno empieza con esquemas de mates y no para de encontrar ideas dinámicas. En Minute Labs han realizado un espectacular generador de patrones que localizan e ilustran la posición de los números primos, de fibonacci, primos de fibonacci, sumas de fibonacci, de carmichael, ternas pitagóricas… y hasta al azar o con el término general que se quiera de cualquier sucesión. Y salen, a elegir, en cuadrícula, espiral de Ullam, de Vogel, en triángulo o pirámide y con el color y zoom que se desse. Todo en Number Constellations. Impresionante.
Nubes de números en la constelación de la edición 5.1 del Carnaval de Matemáticas en titoeliatrondixit.

Publicado el por
3

CUADRADO MAGICO
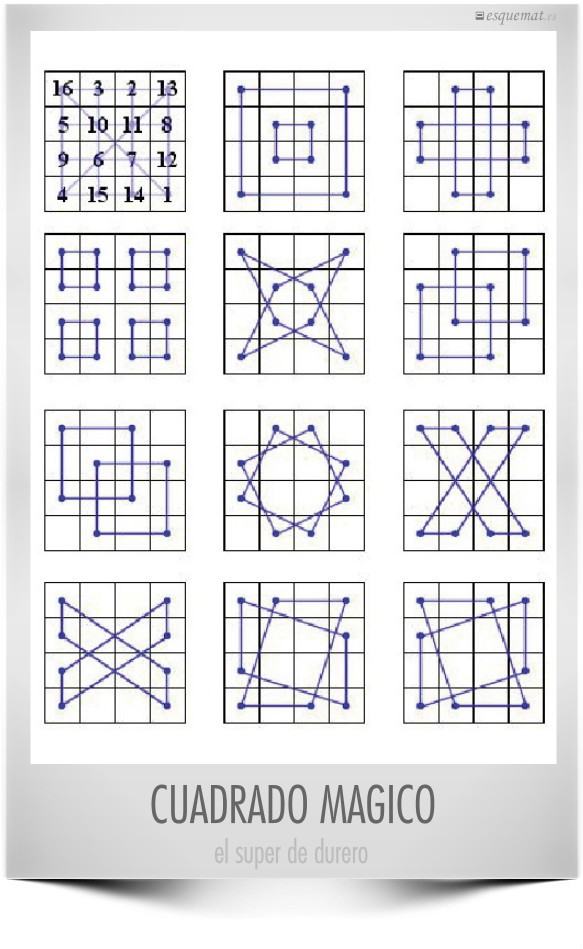
En el cuadrado supermágico de Durero las filas, las columnas y las diagonales suman 34 Pero también los vértices, los números del centro y así hasta las 34 líneas de 4 números de la imagen superior, publicada en The Story of Mathematics. Y hay más sumas que dan 34. De ahí que llamen supermágico al cuadrado de Durero. Todo un artista.
Y más de 34 34’s encuentra, ilustra y comenta @gaussianos en El cuadrado mágico del pintor y acaba proponiendo analizar los cuadrados con los cuadrados y los cubos de los números del de Durero, Y enriquece el tema en La gran belleza de los cuadrados mágicos aportando otros 14 de diversos tamaños y hasta de letras y figuras.
Por su parte @druizaguilera reivindica al escultor Josep Mª Subirachs como autor del cuadrado mágico en la catedral de Gaudí, que admite 310 posibilidades de sumar 33 con 4 casillas, 33 de las cuales podemos ver en el esquemat inferior, con un gráfico del mismo Subirachs. ¡Todo un reto hallar los 310!
Esta entrada participa en la edición 4.1231056 del Carnaval de Matemáticas alojado en Scientia.

CUADRADO MAGICO EN BCN

Publicado el por
1

NUMEROS
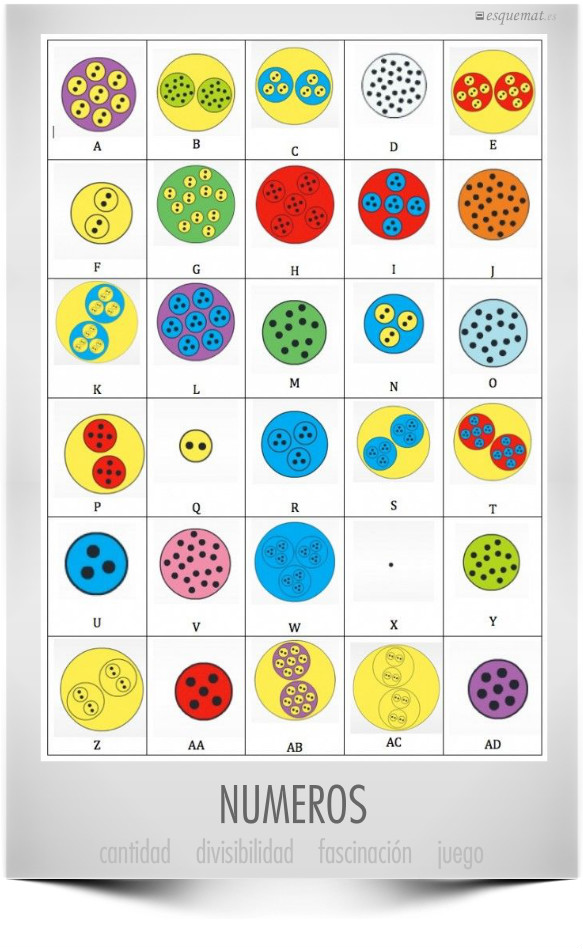
El fascinante mundo de los números presentado de forma fascinante, con 2³.5³ maneras de mirar, buscar, razonar y jugar con ellos. Jim Noble nos dice que “nuestro sistema de numeración está tan abarrotado de patrones y misterios que podríamos pasar toda una vida explorándolos todos. Y él lo hace.
Sin mirar la solución, se puede jugar primero a encontrar los números, a ver cuantos, a ¿por qué los colores? y mucho más en las hojas que presenta en Prime Pictures. Editadas en word para que cada profe las adapte a su gusto y con hojas de soluciones.
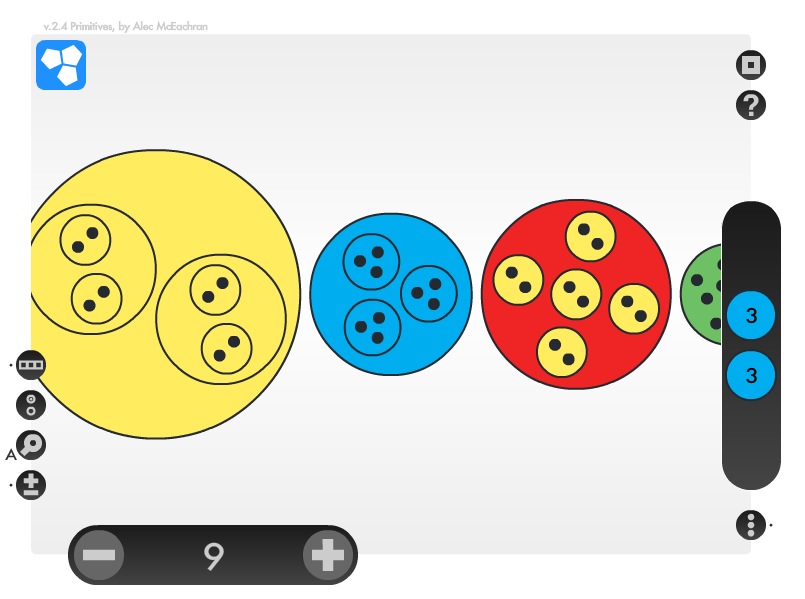
Y después de descubrir, desmenuzar y disfrutar con ello podemos ir a la App Primitives de Alec McEachran, que es la base inspiradora del asunto y donde se generan los números con sus colores y factorizaciones. Para muestra el 9, entre el 8 y el 10. ¡Increíble!

Esta entrada participa en la edición 4.123105 del Carnaval de Matemáticas en Cifras y Teclas.

Publicado el por
1

Number tree
Increíble presentación de los números del 1 al 100 basada en la divisibilidad. La relación divide a es de orden parcial y se representa en un árbol. El innovador, artista y programador Jeffrey Ventrella ha programado este árbol  que se forma según caen del cielo los números enteros. Cada uno se coloca unido a sus divisores, de forma que los números primos abren rama, desde el 1 y los compuestos se unen al mayor de sus divisores (unir todos los divisores crearía confusión gráfica). Todo en acción con un movimiento fascinante en ventrella.com/numbertree.
Esta entrada participa en la edición 4.123105 del Carnaval de Matemáticas en Cifras y Teclas.

SUMA DE NUMEROS IMPARES
La suma de números impares consecutivos va dando cuadrados perfectos: 1 + 3 + 5 +…+ (2n-1) = n²
Una interesante fórmula que se demuestra por inducción y que se ve de manera clara y preciosa en este diagrama. Publicado y comentado en la sección visual maths de catonmat.net.

Publicado el por
1

REGULARIDADES NUMERICAS
Operaciones que asombran y fascinan y son muy útiles para investigar, buscar regularidades y encontrar propiedades que expliquen resultados tan vistosos como estos. Visto en el pinterest de efonsmaldonado.

Publicado el por
1

REGLAS DE DIVISIBILIDAD
Las reglas básicas de divisibilidad en una chuleta clara y colorista que sirve de paso para practicar vocabulario matemático en inglés. Póster a la venta en posterenvy.

Publicado el por
1

TABLAS DE MULTIPLICAR
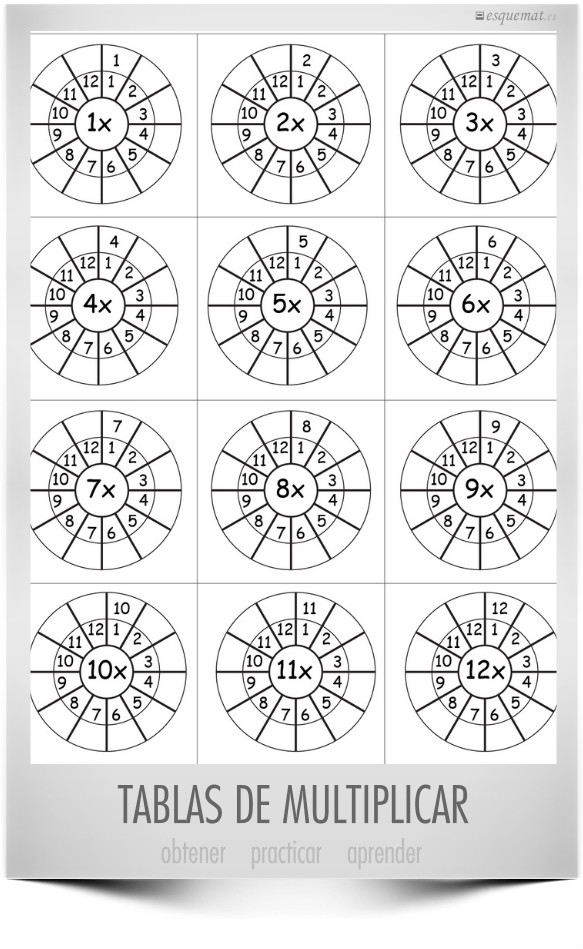
Una sencilla manera de escribir las tablas de multiplicar para practicar con ellas y aprenderlas. Pueden descargarse en worksheetfun.com

Publicado el por
1

TERNAS PITAGORICAS
Una terna pitagórica está formada por 3 números enteros positivos a, b, c que pueden formar un triángulo rectángulo, es decir, que cumplen la fórmula del teorema de Pitágoras a² = b² + c². El gráfico muestra diversos casos ordenados según los estudios realizados en pythagoreantriples, blog especializado en el tema. Un buen tema para dejar que los alumnos investiguen y encuentren ternas y regularidades.

DIFICULTAD EN LA MULTIPLICACION
También usamos esquemas y diagramas sólo para profes. Como este que refleja qué multiplicaciones resultan fáciles o difíciles para los alumnos, según una investigación de The Guardian entre 232 estudiantes de primaria.