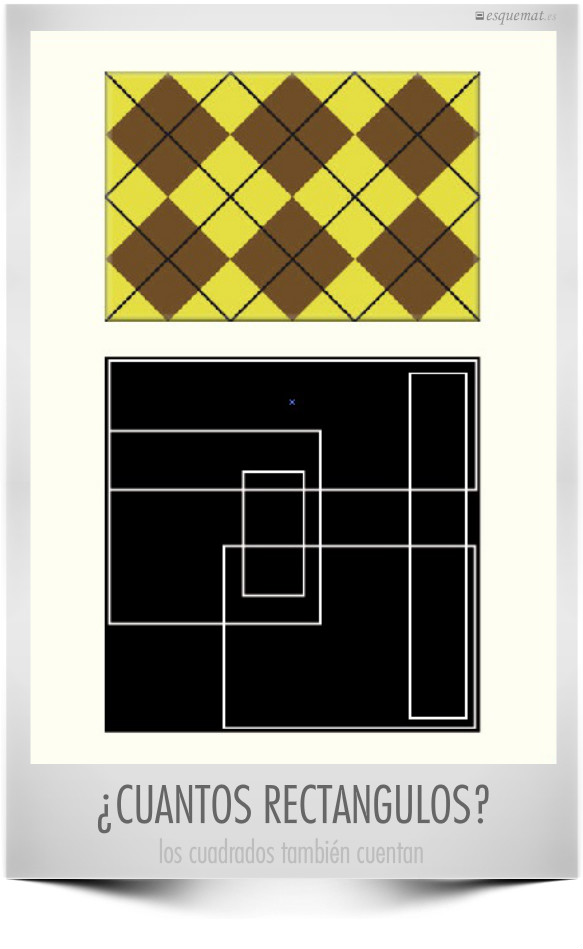
Un problema clásico, que puede plantearse con un fotomat o sobre dibujos geométricos.
Los originales son de transum.org, donde hay una versión pdf, y otras animadas e interactivas.
Clic en la imagen abre el esquemat en pdf.
Archivo de la categoría: proceso

Pintamos de rojo un vértice de un cubo, de verde los vértices que están a 1 arista de distancia, de naranja a 2 y de azul a 3. No es la distancia habitual en línea recta, sino la distancia Manhatan, el camino más corto por las aristas. Con los 4 colores tenemos 16 posibilidades que tienen su reflejo en una función booleana que se ve en la imagen. Los colores ilustran la relación entre los 16 números en base 2, de 0000 (0) a 1111 (15) y los vértices seleccionados cada vez en el cubo.
El autor del esquema, Eiichi Wada explica los detalles y la simetría, aunque, eso sí, en japonés.
Esta entrada participa en la edición 4.1231056 del Carnaval de Matemáticas alojado en Scientia.
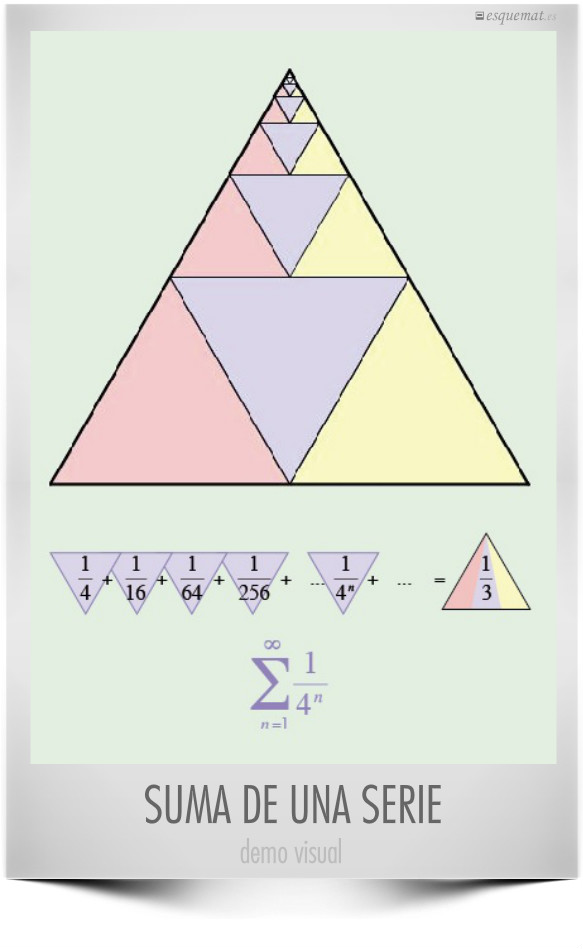
Visualización de la suma de la serie infinita de los inversos de las potencias de 4. La dejamos sin palabras, para que cada uno trate de comprenderlo.
La explicación detallada está en mrhonner.com, publicada el 11/11/11, que llama día del triángulo equilátero, por tener 3 números iguales.
Clic en la imagen abre un pdf con el esquema en A4.
Esta entrada participa en la edición 4.1231056 del Carnaval de Matemáticas alojado en Scientia.
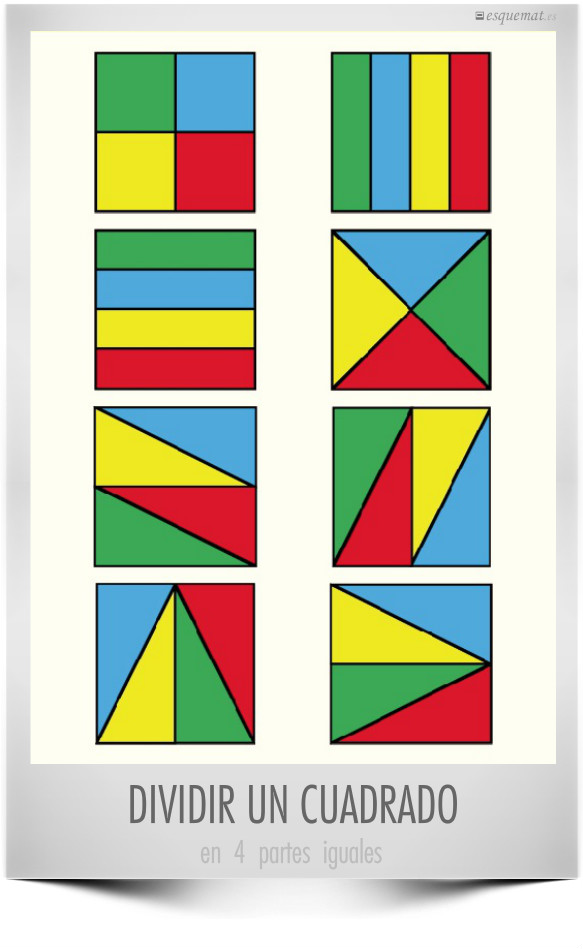
Un ejercicio sencillo para pensar y dejar investigar, dibujar cuadrados y dividirlos en 4 partes iguales. Hay muchas posibilidades y puede hacerse a mano o a máquina, digital, claro. Y se pueden probar otros caso, en 3 partes, en 6, con curvas…
Clic en la imagen abre un pdf con el esquema. Fuente Realm of Maths.
Esta entrada participa en la edición 4.1231056 del Carnaval de Matemáticas alojado en Scientia.

Cualquier método es bueno para ilustrar el Teorema de Pitágoras. Se hace con cuadrados sobre los lados, pero se puede hacer con círculos o piezas de lego o tomates o cualquier figura. La de hoy es muy sabrosa, con crujientes crackers (≈ galletitas): 9 sobre un lado + 16 sobre el otro = 25 en la hipotenusa. ¡Que aproveche! Publicado en el MoMath.
Esta entrada participa en la edición 4.1231056 del Carnaval de Matemáticas alojado en Scientia.
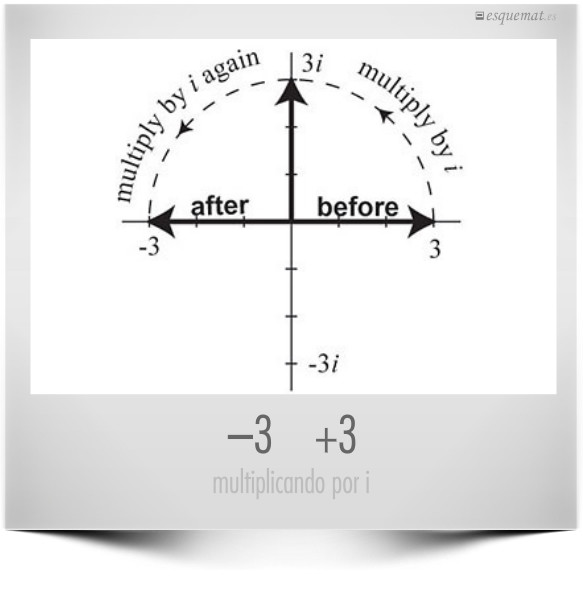
Representamos los números positivos y negativos en una recta, hacia un lado y al otro del origen. Y multiplicar un número por la unidad imaginaria i es como girarlo 90º y si multiplicamos otra vez por i obtenemos el opuesto, lo que es multiplicar en dos veces por –1 o girar 180º.
Cosas complejas que se ven sencillas gráficamente, como en la imagen del artículo Finding your roots de Steven Strogatz.
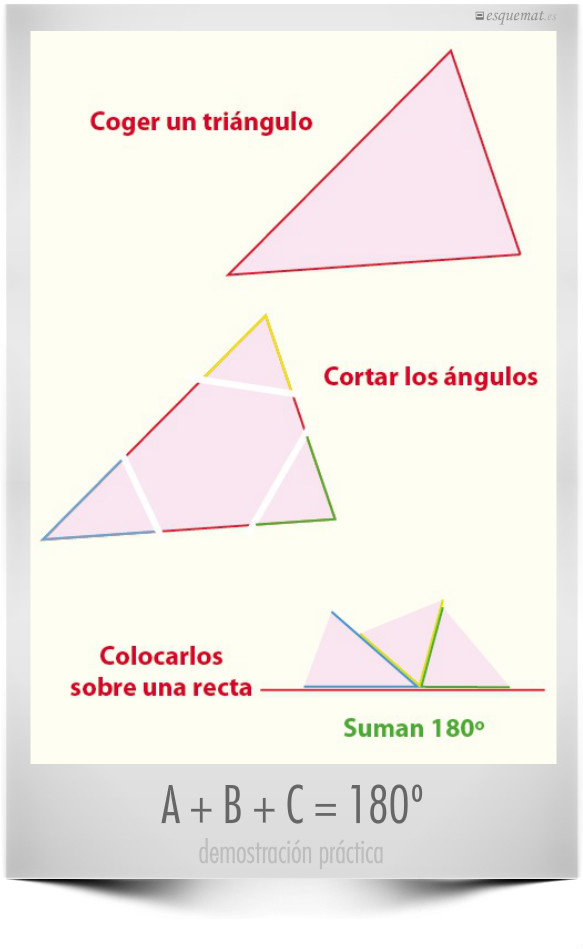
Sencilla y contundente demostración visual de que los 3 ángulos de un triángulo suman 180º. Para todas las edades.
Se puede probar con distintos tipos de triángulos, como se puede ver en learnatmathematicsrealm, fuente de la idea.
Clic en la imagen abre la demo en un pdf tamaño A4.

La Bean Machine, Galton Box o máquina Quincunx de Galton, inventada por Sir Francis Galton para demostrar el teorema del límite central, en particular, que la distribución normal se aproxima a la distribución binomial. Publicado en purestform.

Increíble presentación de los números del 1 al 100 basada en la divisibilidad. La relación divide a es de orden parcial y se representa en un árbol. El innovador, artista y programador Jeffrey Ventrella ha programado este árbol que se forma según caen del cielo los números enteros. Cada uno se coloca unido a sus divisores, de forma que los números primos abren rama, desde el 1 y los compuestos se unen al mayor de sus divisores (unir todos los divisores crearía confusión gráfica). Todo en acción con un movimiento fascinante en ventrella.com/numbertree.
Esta entrada participa en la edición 4.123105 del Carnaval de Matemáticas en Cifras y Teclas.

Una buena manera practicar y comprobar en vivo el teorema de Pitágoras.


