Otra forma, más saltarina, de jugar con las fracciones. Inventada por un niño y desarrollada y explicada por su maestra en capturing classroom ideas.
Archivo de la etiqueta: operaciones

Del mismo modo que multiplicando por 8 sale una bonita pirámide, al hacerlo por 9 obtenemos esta.

Operaciones que asombran y fascinan y son muy útiles para investigar, buscar regularidades y encontrar propiedades que expliquen resultados tan vistosos como estos. Visto en el pinterest de efonsmaldonado.
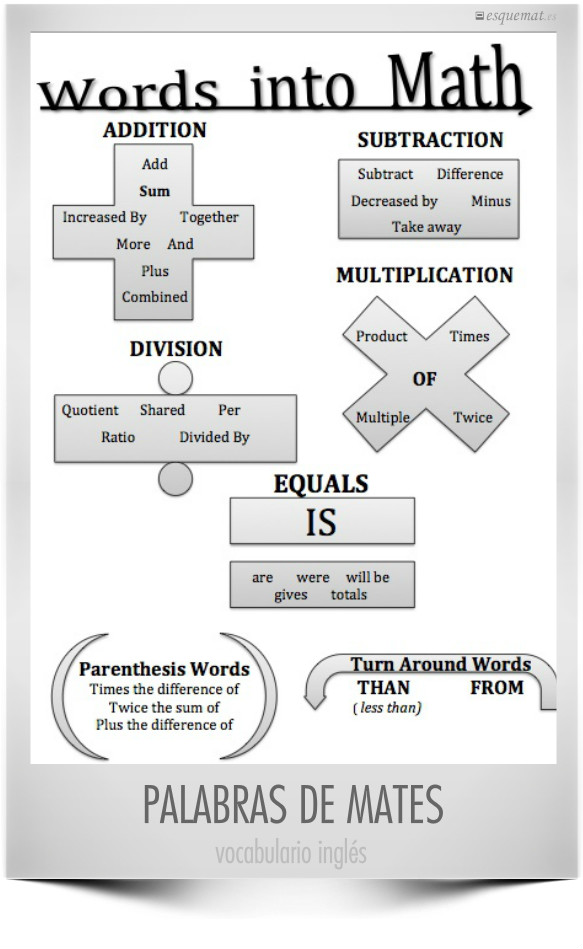
Distintas palabras inglesas relacionadas con operaciones y símbolos matemáticos.
Publicado en ispeakmath.
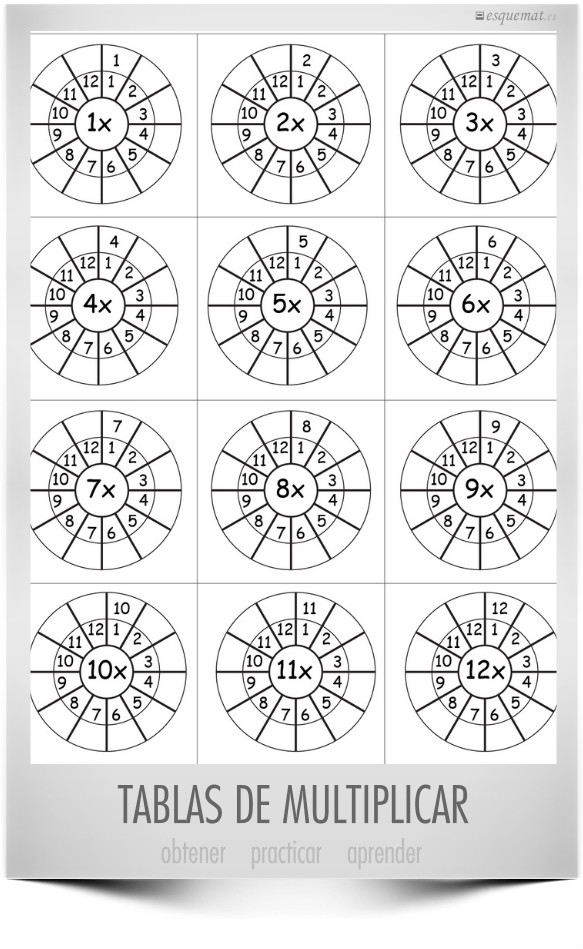
Una sencilla manera de escribir las tablas de multiplicar para practicar con ellas y aprenderlas. Pueden descargarse en worksheetfun.com

También usamos esquemas y diagramas sólo para profes. Como este que refleja qué multiplicaciones resultan fáciles o difíciles para los alumnos, según una investigación de The Guardian entre 232 estudiantes de primaria.
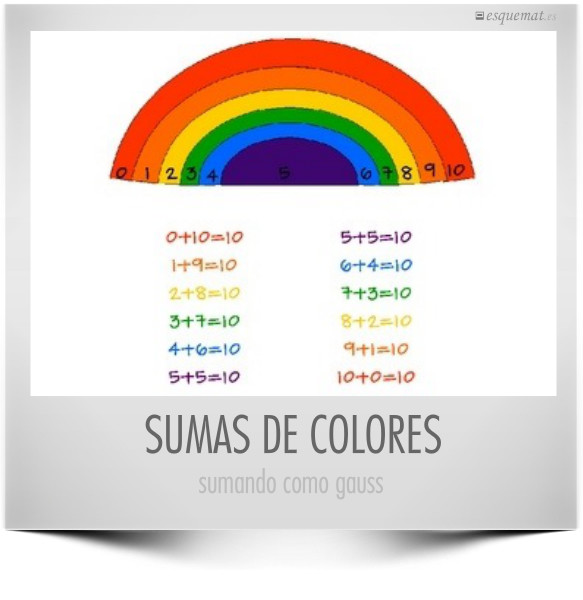
La señorita Kindergarten presenta en su blog divertidos recursos para las mates de los más pequeños. Como este arco iris para sumar y reflexionar sobre la simetría de los números de una progresión acercando a los niños a lo que ya descubrió Gauss a sus 10 años y que sirve de paso para descubrir los recursos y materiales del portal teacherspayteachers.
Clic en la imagen abre plantillas del arco iris 10 en pdf para usar en clase.
Esta entrada participa en la edición 4.123 del Carnaval de Matemáticas en el blog Eulerianos.
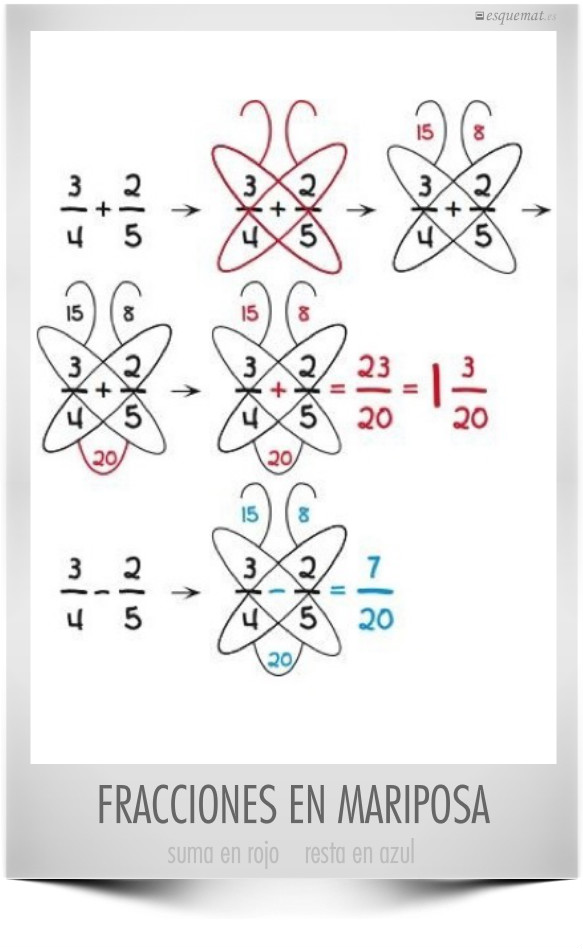
Un original método para enseñar a sumar y restar fracciones a los más pequeños.
Difundido por Sarah Moran en pinterest.

Criba de Eratóstenes realizada con diseño especial, hecha en LaTex, con polígonos que ilustran los múltiplos de cada nº primo.
Fuente TikZGallery en khaos.github.com

Si ayer veíamos un complejo diseño de diagramas de Venn de 7 conjuntos de colores, que es todo un logro, hoy la cosa se supera con 11. Es muy difícil porque un diagrama de Venn debe mostrar todas las intersecciones posibles. Para verlo claro se intenta hacerlo simétrico ( invariante bajo rotación, hasta un reetiquetado de curvas) y simple (no se cortan más de dos curvas en un punto). La pregunta desde 1960 era si ambas cosas son posibles con un número primo de conjuntos mayor que 3.
Khalegh Mamakani y Ruskey Frank, de la Universidad de Victoria en British Columbia, con geometría computacional presentan una nueva propiedad de los diagramas de Venn llamada simetría de corte transversal y encontraron muchos diagramas de Venn simples simétricos con 11 curvas. El primero de ellos es el de la imagen.
Esta entrada participa en la Edición 4.12 del Carnaval de Matemáticas en el blog High Ability Dimension