
El gusto por la geometría también está presente en la publicidad, como en este cartel de sonarmática para microbcn que hueja con polígonos, diagonales y proyecciones.

Si ayer veíamos un complejo diseño de diagramas de Venn de 7 conjuntos de colores, que es todo un logro, hoy la cosa se supera con 11. Es muy difícil porque un diagrama de Venn debe mostrar todas las intersecciones posibles. Para verlo claro se intenta hacerlo simétrico ( invariante bajo rotación, hasta un reetiquetado de curvas) y simple (no se cortan más de dos curvas en un punto). La pregunta desde 1960 era si ambas cosas son posibles con un número primo de conjuntos mayor que 3.
Khalegh Mamakani y Ruskey Frank, de la Universidad de Victoria en British Columbia, con geometría computacional presentan una nueva propiedad de los diagramas de Venn llamada simetría de corte transversal y encontraron muchos diagramas de Venn simples simétricos con 11 curvas. El primero de ellos es el de la imagen.
Esta entrada participa en la Edición 4.12 del Carnaval de Matemáticas en el blog High Ability Dimension

No hay mejor esquemat que los diagramas de Venn para representar conjuntos y sus propiedades. Es facil usarlos para dos conjuntos ó si son 3 ó 4, pero la cosa se va complicando cuando el número va en aumento y se quiere representar todas las posibles intersecciones.
Con números con cifras del 1 al 7 David McCandless presenta un increíble diagrama con las intersecciones de 7 conjuntos, cada uno con los números en los que sale una cifra.
Y Santiago Ortiz lo hace maravilloso, variable e interactivo cambiando los números por puntos de los 7 colores del espectro de Newton a los que nombra según esta lista de colores.
Como en la imagen superior, se puede elegir 1 color, 2, 3 … 7, viendo al instante el conjunto de cada color con todas sus intersecciones, hasta 128 = 2⁷ en el caso máximo. Se obtienen imágenes fascinantes, porque además se puede girar todo y observar los conjuntos coloreados completamente siendo las intersecciones las mezclas de los 7 colores. ¡Para no perdérselo!
Esta entrada participa en la Edición 4.12 del Carnaval de Matemáticas en el blog High Ability Dimension
Chuleta con las formas y nombres en inglés de las figuras geométricas planas, especial para los más pequeños. Convertidas en personajes, sirven además para crear historias con ellas en un aprendizaje divertido y creativo. Diseñado por Laura Martin.
Esta entrada participa en la Edición 4.12 del Carnaval de Matemáticas en el blog High Ability Dimension
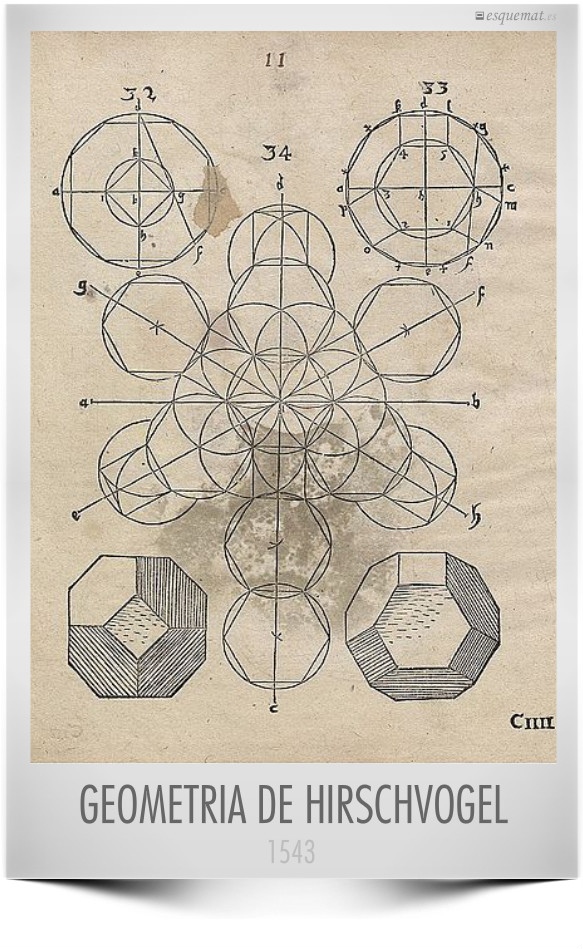
Página del libro Geometria de Augustin Hirschvoge, artista alemán, matemático y cartógrafo, volúmen conservado en la biblioteca de la Universidad de Dresde.
La búsqueda de la belleza, armonía y perfección artística llevó a complejos estudios geométricos como expone el libro La ciencia del arte.
Esperemos poder corresponder dando mayor arte, belleza y claridad a los formularios y diseños matemáticos, como podemos ver, rever y no cansarnos de ver en la obra de Cristobal Vila que divulgó las imágenes de este libro, que me llegó gracias a @SilviaP3.
Esta entrada participa en la Edición 4.12 del Carnaval de Matemáticas en el blog High Ability Dimension
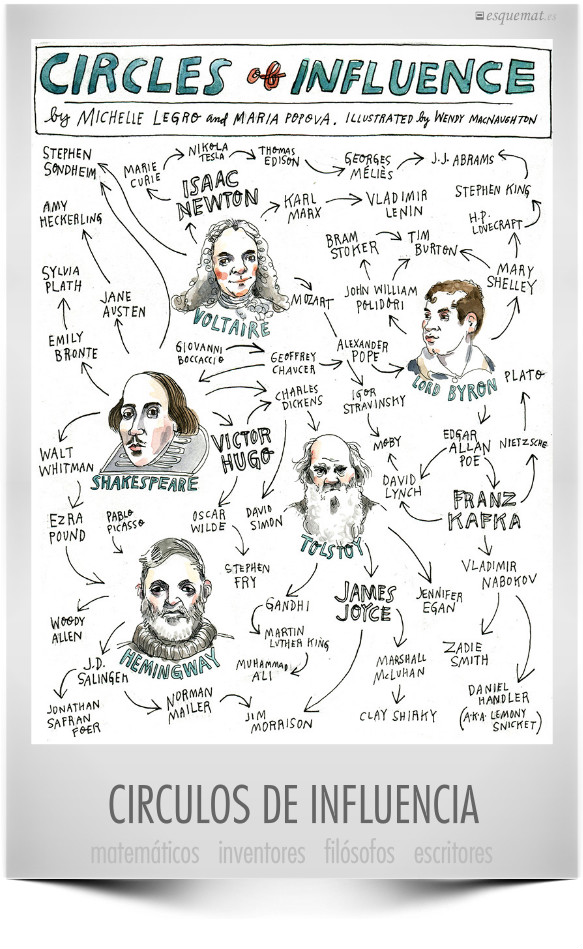
Las matemáticas no sólo sirven para muchas cosas y están en casi todo, sino que, como todo lo demás, ejercen una gran influencia en su tiempo en todo tipo de personas. El mundo no hubiera sido igual sin Newton.
Este gráfico lo muestra, no de un modo científico riguroso, pero sí desde un análisis de la vida y obra de los distintos personajes. Está realizado por la ilustradora Wendy MacNaughton, la creativa Maria Popova y la editora Michelle Legro y se publicó en la revista Longshot.
Esta entrada participa en la Edición 4.12 del Carnaval de Matemáticas en el blog High Ability Dimension
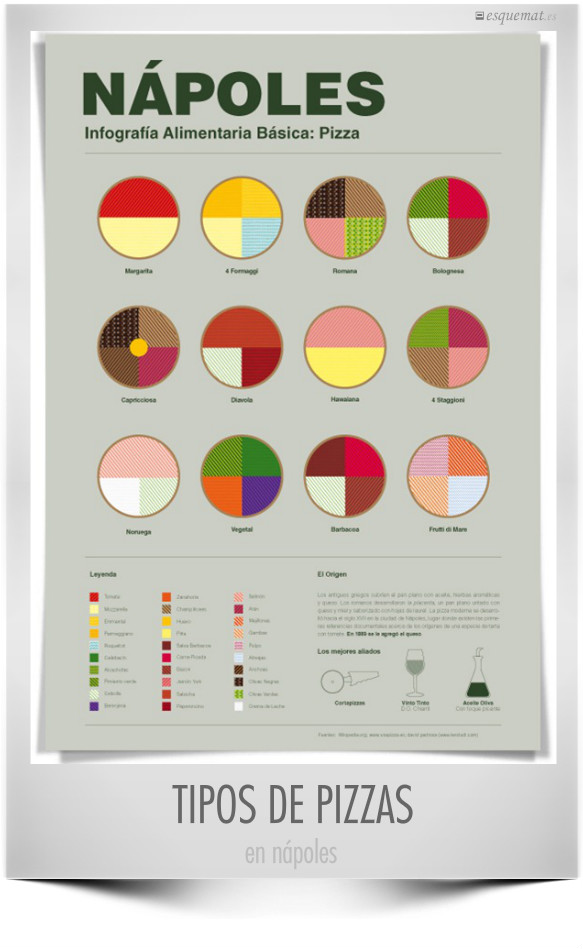
Porque también los matemáticos necesitamos comer y los cocineros expresarse. Aqui tenemos un bonito esquema de los tipos de pizza en Nápoles, obra de @lesstudi, que ha realizado también infografías similares de sushi, hamburguesas, pintxos y sandwitchs presentes en 5 ciudades del mundo.
Esta entrada participa en la Edición 4.12 del Carnaval de Matemáticas en el blog High Ability Dimension

Diagrama horizontal que ilustra el intervalo de sonidos de los distintos instrumentos musicales medidos según las notas de la escala y sus correspondientes frecuencias en hertzios. Las C1 … C7 del teclado corresponden en notación americana a las notas do₁ … do₇ siendo en este caso el C4 el do central. El estudio matemático de notas y frecuencias contribuyó a perfeccionar el diseño de los pianos y en toda la concepción teórica de la música y el sonido. Fuente nodomutante.
Clic en la imagen abre un gif de gran tamaño.
Esta entrada participa en la Edición 4.12 del Carnaval de Matemáticas en el blog High Ability Dimension
La fotografía matemática es un buen recurso de visualización que permite alegrar el estudio y mejorar la comprensión.
Celebramos hoy las 500 fotos, ∞ matemáticas en nuestro fotomat.es con un poster con las 500 miniaturas, que se convierte en un laaargo pdf al clicar en la imagen.




