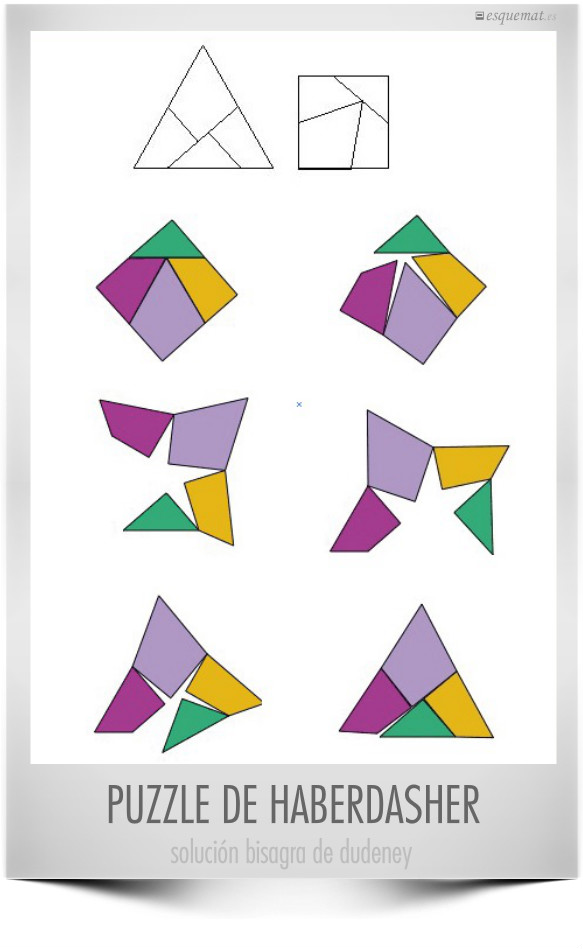
El problema de Haberdasher, cortar un triángulo equilátero en cuatro piezas que formen también un cuadrado, resuelto elegantemente por Henry Dudeney con las piezas unidas por el vértice que, a modo de bisagras, pueden girar para pasar de una figura a la otra.
Expresado en gif animado con código por matthen, inspirado en la versión interactiva de wolframalpha. Espectacular.
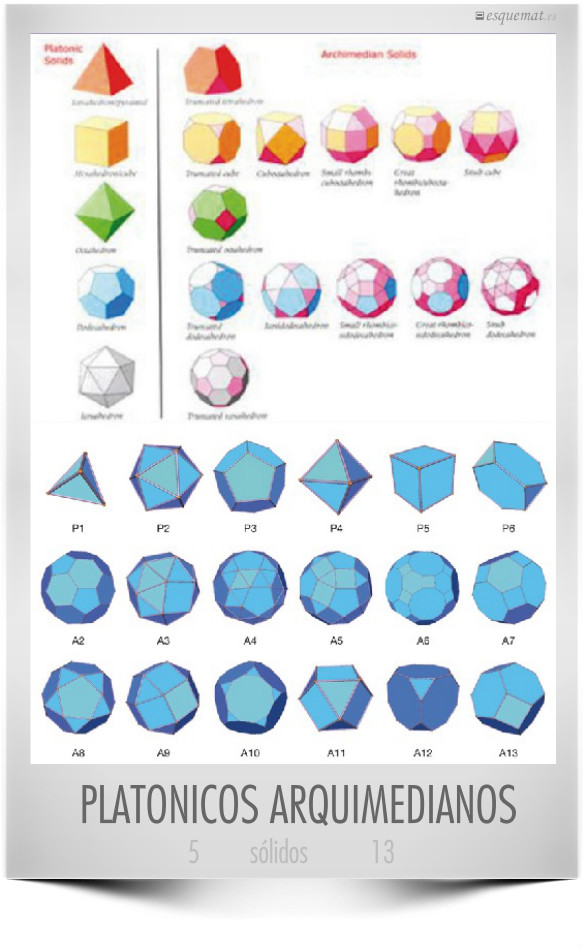
Dos visiones de los 5 sólidos platónicos, tetraedro, icosaedro, dodecaedro, octaedro y cubo, y los 13 arquimedianos, tetraedro truncado (A1), icosaedro truncado (A2), cubo chata (A3), desaire dodecaedro (A4), rombicosidodecaedro (A5), truncada icosidodecaedro (A6), truncada cuboctaedro (A7), icosidodecaedro (A8 ), rombicuboctaedro (A9), dodecaedro truncado (A10), cuboctaedro (A11), el cubo truncado (A12) y octaedro truncado (A13). Publicados en nature.
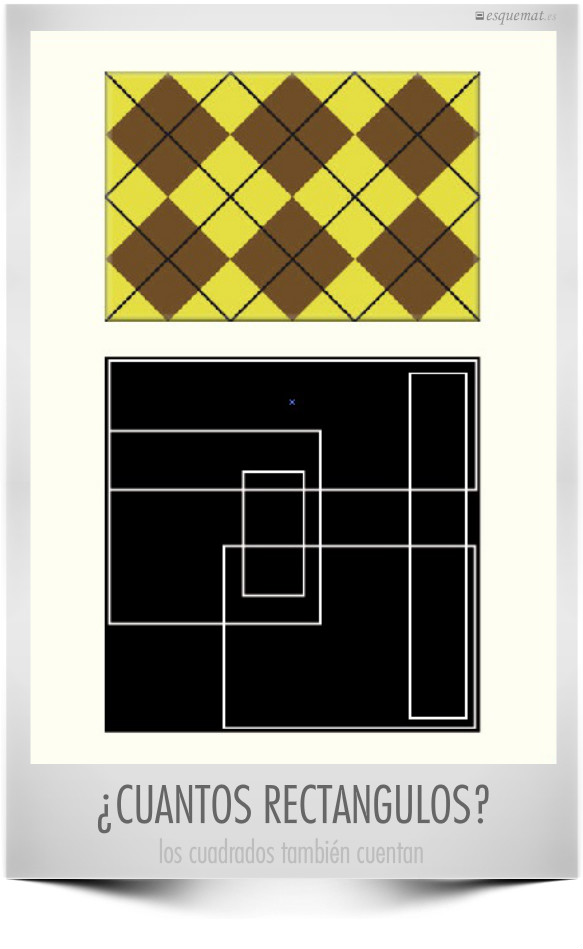
Un problema clásico, que puede plantearse con un fotomat o sobre dibujos geométricos.
Los originales son de transum.org, donde hay una versión pdf, y otras animadas e interactivas.
Clic en la imagen abre el esquemat en pdf.

Composiciones originales inspiradas en la Topología y Topografía. Hay varios, muy hermosos, en surfacearea.org.

Pintamos de rojo un vértice de un cubo, de verde los vértices que están a 1 arista de distancia, de naranja a 2 y de azul a 3. No es la distancia habitual en línea recta, sino la distancia Manhatan, el camino más corto por las aristas. Con los 4 colores tenemos 16 posibilidades que tienen su reflejo en una función booleana que se ve en la imagen. Los colores ilustran la relación entre los 16 números en base 2, de 0000 (0) a 1111 (15) y los vértices seleccionados cada vez en el cubo.
El autor del esquema, Eiichi Wada explica los detalles y la simetría, aunque, eso sí, en japonés.
Esta entrada participa en la edición 4.1231056 del Carnaval de Matemáticas alojado en Scientia.
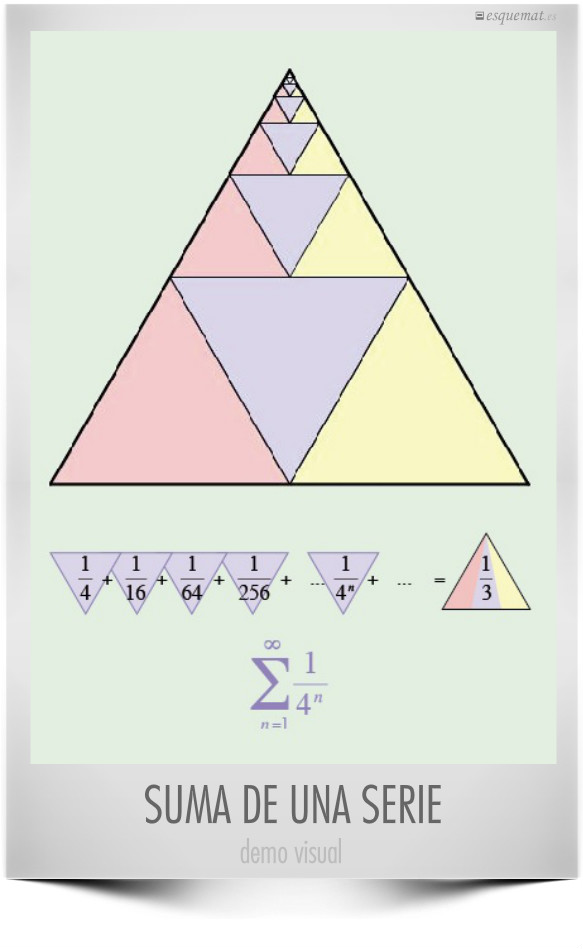
Visualización de la suma de la serie infinita de los inversos de las potencias de 4. La dejamos sin palabras, para que cada uno trate de comprenderlo.
La explicación detallada está en mrhonner.com, publicada el 11/11/11, que llama día del triángulo equilátero, por tener 3 números iguales.
Clic en la imagen abre un pdf con el esquema en A4.
Esta entrada participa en la edición 4.1231056 del Carnaval de Matemáticas alojado en Scientia.

Uniendo forma y contenido en un hermoso diseño de Waterboy1992.
Esta entrada participa en la edición 4.1231056 del Carnaval de Matemáticas alojado en Scientia.
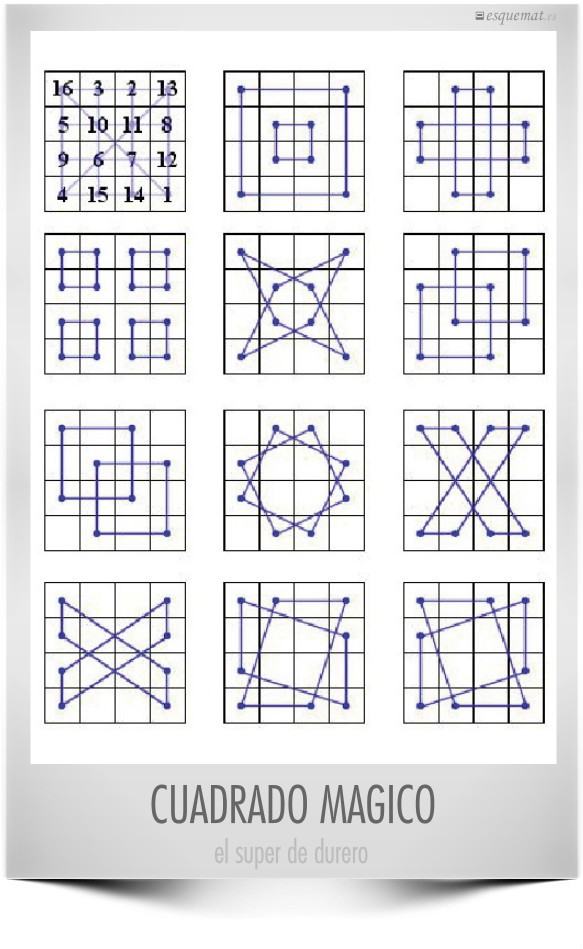
En el cuadrado supermágico de Durero las filas, las columnas y las diagonales suman 34 Pero también los vértices, los números del centro y así hasta las 34 líneas de 4 números de la imagen superior, publicada en The Story of Mathematics. Y hay más sumas que dan 34. De ahí que llamen supermágico al cuadrado de Durero. Todo un artista.
Y más de 34 34’s encuentra, ilustra y comenta @gaussianos en El cuadrado mágico del pintor y acaba proponiendo analizar los cuadrados con los cuadrados y los cubos de los números del de Durero, Y enriquece el tema en La gran belleza de los cuadrados mágicos aportando otros 14 de diversos tamaños y hasta de letras y figuras.
Por su parte @druizaguilera reivindica al escultor Josep Mª Subirachs como autor del cuadrado mágico en la catedral de Gaudí, que admite 310 posibilidades de sumar 33 con 4 casillas, 33 de las cuales podemos ver en el esquemat inferior, con un gráfico del mismo Subirachs. ¡Todo un reto hallar los 310!
Esta entrada participa en la edición 4.1231056 del Carnaval de Matemáticas alojado en Scientia.
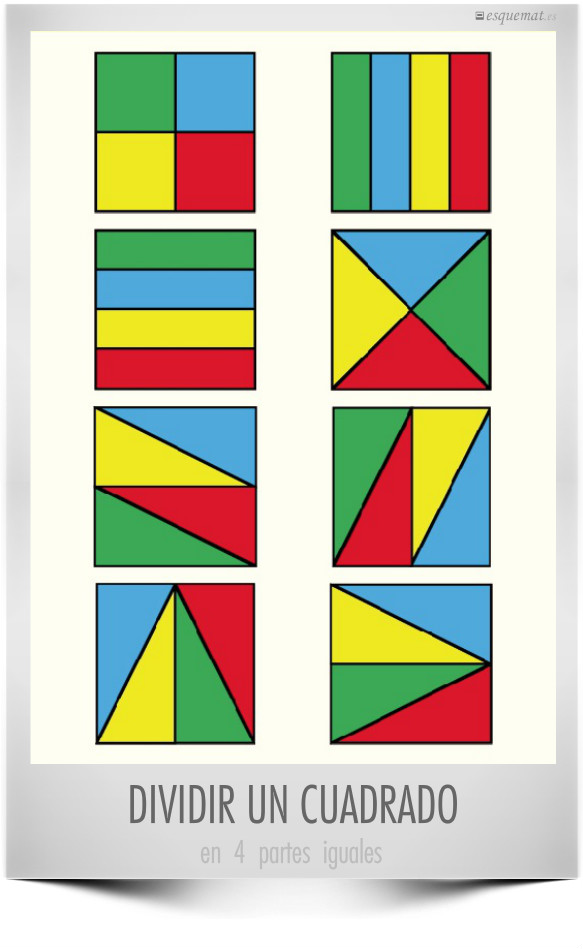
Un ejercicio sencillo para pensar y dejar investigar, dibujar cuadrados y dividirlos en 4 partes iguales. Hay muchas posibilidades y puede hacerse a mano o a máquina, digital, claro. Y se pueden probar otros caso, en 3 partes, en 6, con curvas…
Clic en la imagen abre un pdf con el esquema. Fuente Realm of Maths.
Esta entrada participa en la edición 4.1231056 del Carnaval de Matemáticas alojado en Scientia.

Cualquier método es bueno para ilustrar el Teorema de Pitágoras. Se hace con cuadrados sobre los lados, pero se puede hacer con círculos o piezas de lego o tomates o cualquier figura. La de hoy es muy sabrosa, con crujientes crackers (≈ galletitas): 9 sobre un lado + 16 sobre el otro = 25 en la hipotenusa. ¡Que aproveche! Publicado en el MoMath.
Esta entrada participa en la edición 4.1231056 del Carnaval de Matemáticas alojado en Scientia.



