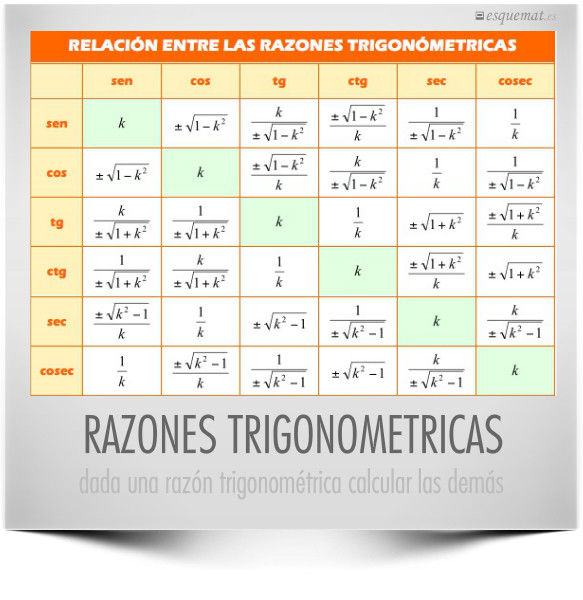
El problema: Se trata de hallar la ecuación de una recta a partir de dos datos (punto-vector, punto-punto, punto-pendiente ó punto-ángulo con OX) o bien de pasar de un modo de ecuación de la recta a otro a partir de esos datos o de alguna de las ecuaciones de la recta.
La herramienta: Un formulario direccional diseñado para consultar fórmulas junto al proceso más simple de utilizarlas. Para cada caso posible los datos están en verde y las incógintas a obtener en rojo. La tabla presenta las fórmulas y las flechas el camino a seguir, a veces pasando de un caso de datos a otro y siguiendo por él.
La técnica: Uno de los datos será necesariamente un punto, llamado (x₀,y₀) en el formulario. Se elige en la tabla la fila que corresponda al otro dato y a partir de él se aplican las fórmulas siguiendo el camino marcado hasta llegar al modo de ecuación deseado.
Con este cuadro pueden obtenerse todas las formas de ecuación de la recta a partir de dos datos o una ecuación.
La experiencia: Con este sistema mis clases de geo analítica cambiaron. Los conceptos se aclaran y los resultados llegan rápidamente. Es muy apreciado por los alumnos porque ayuda a organizar las ideas y salir del lío de tantas fórmulas y conceptos nuevos. El cuadro se va desarrollando en clase, a medida que se avanza en el tema, y luego pueden plantearse ejercicios a tabla vacía, quitando las fórmulas y sustituyendo los datos genéricos por números. Y proponiendo como examen completar un cuadro similar con nuevos datos los resultados han sido espectaculares en alumnos de 15 y 16 años.
El análisis: Como en todos los métodos muy guiados o de plantilla esto puede ser como aprender a andar con takataka y conducir a obtener resultados por imitación sin entender casi nada. El peligro es cierto, si sólo se usan estos métodos, igual que si la enseñanza se limita a cálculos y operaciones, pero si se combinan con creatividad y dinamismo para despertar curiosidad e iniciativa, los esquemas y formularios direccionales se convierten en aliados que recuerdan caminos y ahorran tareas pesadas y rutinarias. La misma realización colectiva de este formulario, buscando reducir al máximo datos y expresiones es muy formativa pues la síntesis requiere gran comprensión. El desafío es hacer y enseñar a hacer herramientas que permitan algo tan matemático como lograr el máximo de posibilidades con el mínimo de recursos.
Material: Clic en la imagen abre un pdf en A4 con el formulario y dos plantillas vacías, en color y b/n, para proponer y resolver ejercicios o exámenes.
Esta entrada participa en la edición 3.1415926535 del Carnaval de Matemáticas cuyo blog anfitrión es La Aventura de la Ciencia.