Construyendo cuadrados sobre los lados de un triángulo rectángulo en un proceso reiterado se obtiene un árbol de Pitágoras, un fractal que toma diversas formas según sea el triángulo inicial. El de la figura, muy bien resuelto, llega al orden 8 y alcanza bastante más en el gif animado original de scipsy:
Árbol de Pitágoras de scipsy
Una terna pitagórica está formada por 3 números enteros positivos a, b, c que pueden formar un triángulo rectángulo, es decir, que cumplen la fórmula del teorema de Pitágoras a² = b² + c². El gráfico muestra diversos casos ordenados según los estudios realizados en pythagoreantriples, blog especializado en el tema. Un buen tema para dejar que los alumnos investiguen y encuentren ternas y regularidades.
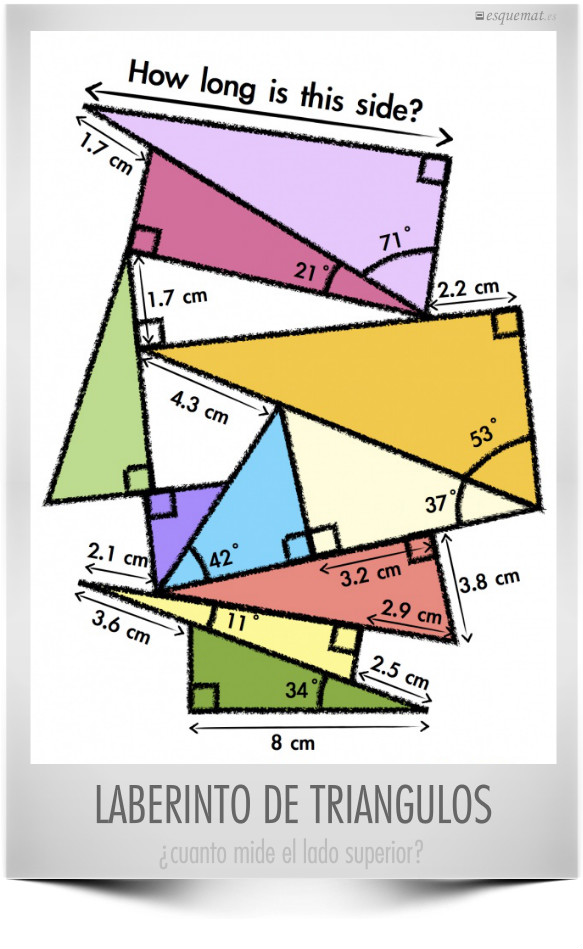
Partiendo de la base de 8 cm y con los datos de ángulos y segmentos que ofrece el dibujo hay que ir ascendiendo poco a poco hasta obtener la medida del lado superior, usando la trigonometría basica y el teorema de Pitágoras. Una idea interesante y efectiva que he utilizado desde hace años en mis clases, aunque no con un diseño gráfico tan logrado como este de greatmathsteachingideas.
Entrada para la Edición 4.1231 del Carnaval de Matemáticas en el blog i-matemáticas.com de JGM.
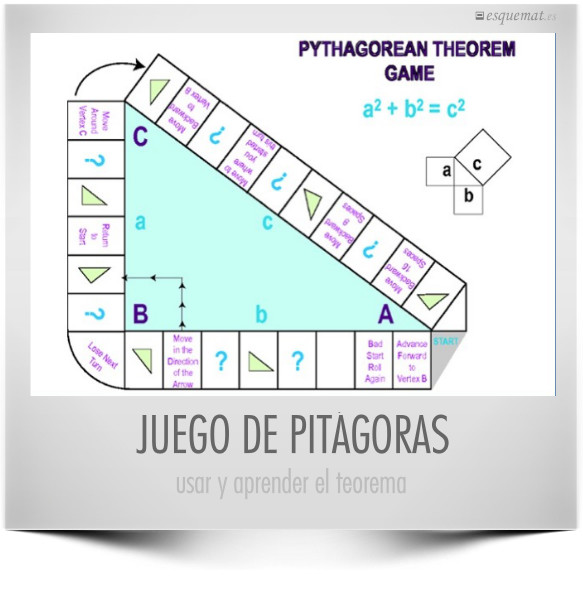
Con ideas del juego de la oca y añadiendo preguntas tenemos este juego del teorema de Pitágoras que alegrará muchas clases. El juego y las reglas son de en gnowledge.org y nos llegan desde el pinterest de la profesora @majitomat con quien desde hace tiempo pasamos muy buenos tuits. ¡Gracias!
Puede tomarse la idea para inventar nuevos juegos de distintos temas. Los alumnos mismos pueden desarrollar juegos con lo que además de las mates pondrán a prueba su imaginación y creatividad.
Formulario para resolver cualquier triángulo: Dados 3 datos (lados o ángulos) se deben hallar los otros 3 datos y el área. Cada fila es uno de los casos posibles y en ella se presentan las fórmulas correspondientes, que son los teoremas del seno y del coseno
Material: Clic en la imagen abre un pdf en A4 con el formulario y plantillas con datos de ejemplo y vacías, para proponer y resolver ejercicios o exámenes.
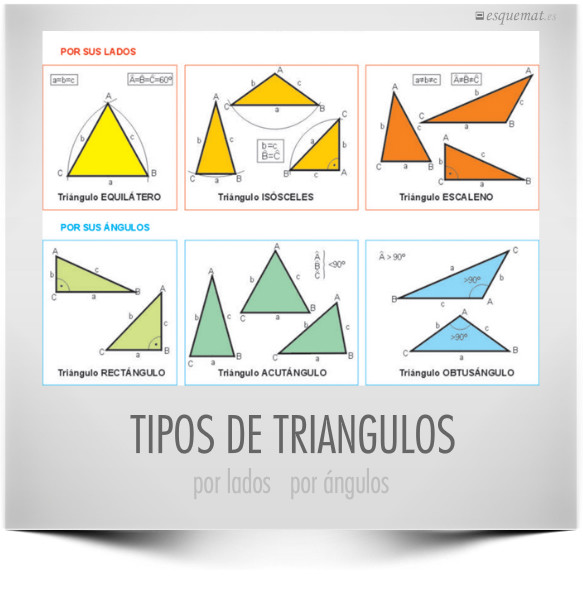
Sencillo esquema sobre los tipos de triángulos publicado junto a un applet en geogebra.es
Formulario para resolver un triángulo rectángulo: Dados 3 datos (uno de ellos el ángulo recto A=90º) se deben hallar los otros 3 datos y el área. Cada fila es uno de los casos posibles y en ella se presentan las fórmulas correspondientes, que son las definiciones de seno, coseno y tangente y el teorema de Pitágoras.
El problema es sencillo con estas fórmulas y un simple dibujo del triángulo, por lo que lo más interesante para practicar y aprender es completar uno mismo este cuadro a partir de una plantilla vacía.
Material: Clic en la imagen abre un pdf en A4 con el formulario y dos plantillas en b/n, una con datos de ejemplo y otra vacía, para proponer y resolver ejercicios o exámenes.
Esta entrada participa en la edición 3.1415926535 del Carnaval de Matemáticas cuyo blog anfitrión es La Aventura de la Ciencia.
Guía:
Clic en la imagen abre una animación que muestra que los dos cuadrados pequeños pequeños llenan el grande.
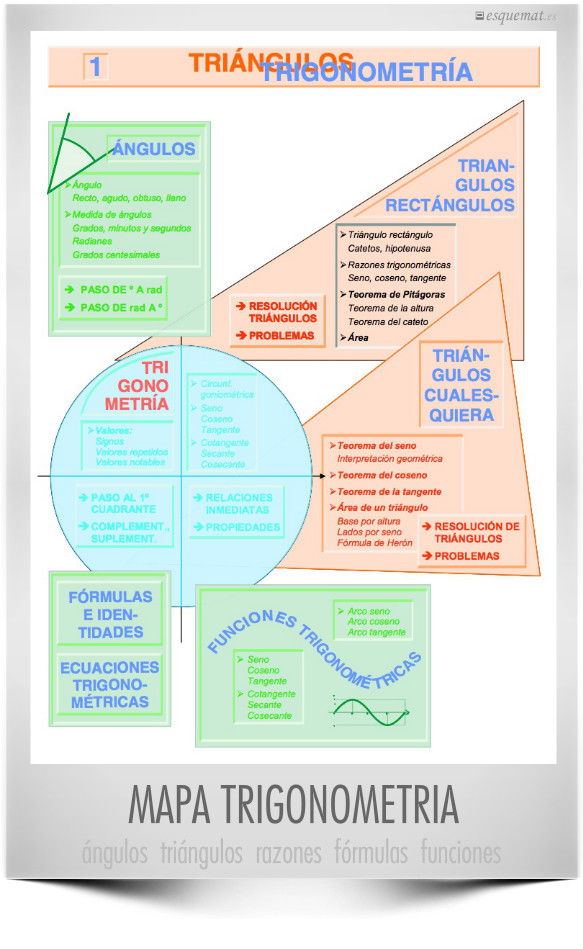
Una visión dinámica de los definiciones, propiedades y cuestiones de la trigonometría y la resolución de triángulos
Guía:
Clic en la imagen abre un pdf para ver, descargar o imprimir.
Guía prof:
El contenido es similar al del esquema de trigonometría. Este estilo mapa ilustra además los contenidos y usos con formas y colores.
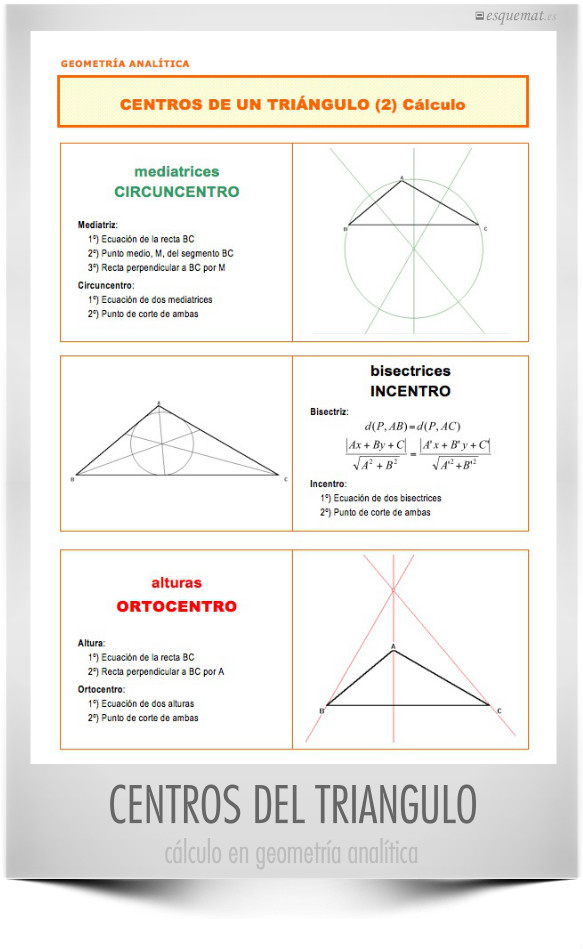
Nombres y gráfica de los centros de un triángulo con indicaciones y fórmulas para encontrar sus coordenadas con ecuaciones de rectas.
Guía:
Clic en la imagen abre el esquema completo de 2 páginas en pdf para ver, descargar o imprimir.
Guía prof:
El es apropiado en geometría analítica, con coordenadas de puntos y ecuaciones de rectas. Para un nivel más sencillo, puede utilizarse los Centros de un triángulo (1) Descripción.
