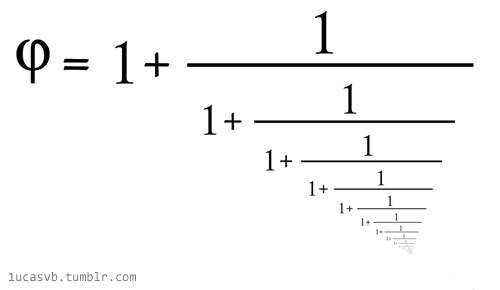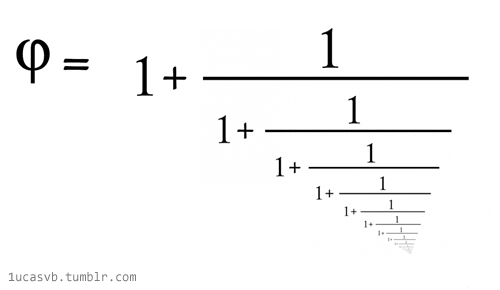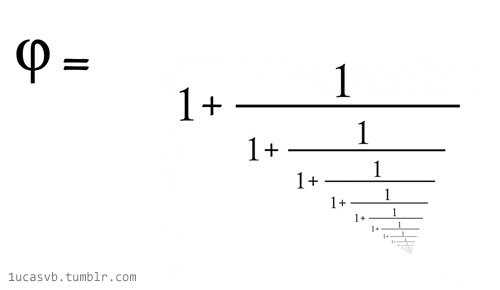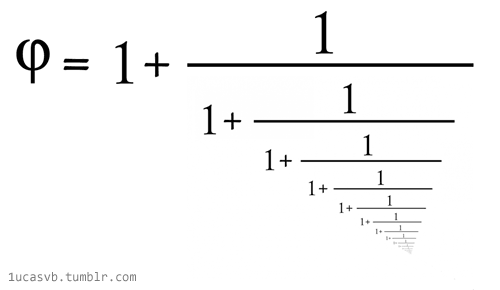The On-Line Encyclopedia of Integer Sequences, iniciada en 1964 por Neil J. A. Sloane, es un recurso tremendo para aprender, investigar, desafiar y disfrutar con sucesiones de números enteros. Contiene 236.488 sucesiones y crece cada día. Está en muchos idiomas, da las reglas de formación, demos, gráficas y música de cada sucesión. Se pueden meter números y encontrará en qué sucesiones están, se pueden descubrir sucesiones históricas, curiosas, divertidas y hasta la de la imagen, 4, 8, 15, 16, 23, 62 que es la de la serie Perdidos.
Esta entrada participa en la edición 4.12310562561 del Carnaval de Matemáticas en cuentos cuánticos
Archivo de la etiqueta: series
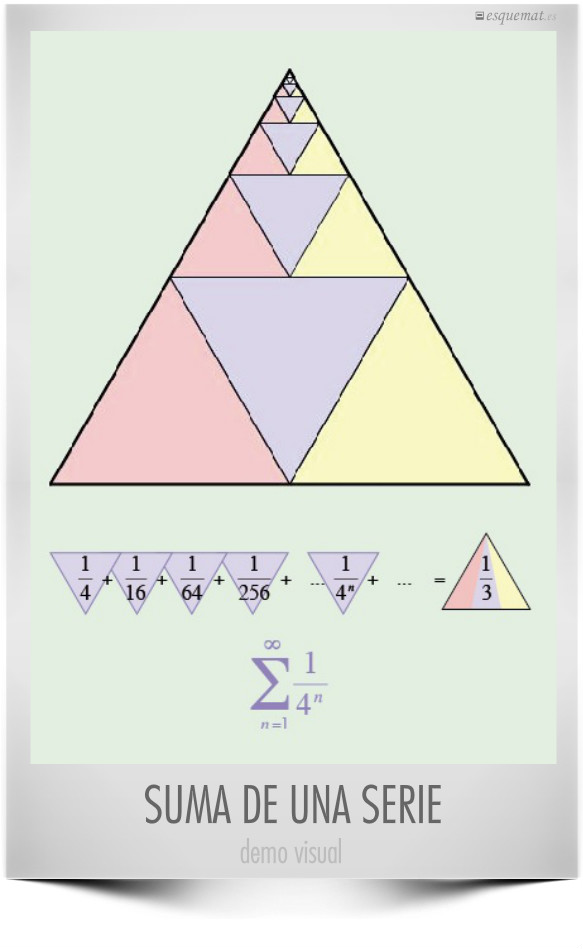
Visualización de la suma de la serie infinita de los inversos de las potencias de 4. La dejamos sin palabras, para que cada uno trate de comprenderlo.
La explicación detallada está en mrhonner.com, publicada el 11/11/11, que llama día del triángulo equilátero, por tener 3 números iguales.
Clic en la imagen abre un pdf con el esquema en A4.
Esta entrada participa en la edición 4.1231056 del Carnaval de Matemáticas alojado en Scientia.

Un juego increíblemente sencillo, divertido y estimulante para la mente. Se empieza pintando libremente cada hexágono de la fila superior de la plantilla de colores, azul, rojo o amarillo.
Y se sigue, fila a fila, con 2 reglas:
1- Si los dos hexágonos anteriores son del mismo color, el hexágono intermedio de la fila siguiente se pinta de ese color.
2-Si los dos hexágonos anteriores son de distinto color, el hexágono intermedio de la fila siguiente se pinta del tercer color.
Se producen multitud de situaciones distintas y se puede jugar a formar figuras, prever el color del vértice y a mil cosas que explican y muestran en pinkmathematics.
La idea original es de Steve Humble, publicada en el New York Times.
Y @Calaix2 recoge el juego en su Blog del Calix +ie en un detallado y bien ilustrado post y amplía el desafío con distintas opciones y materiales. Ánimo y ¡a jugar!
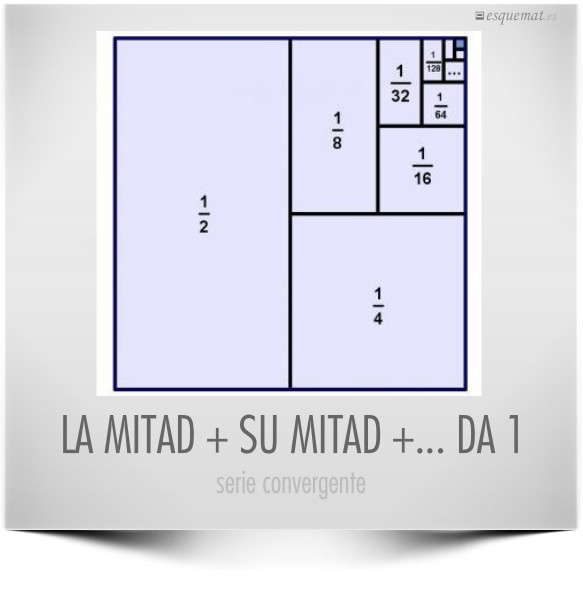
Magnífica demostración visual de que la suma de la serie ½ + ¼ + ¹⁄₈ + ¹⁄₁₆ + … es igual a 1. Porque las cosas no funcionan igual cuando se va al infinito. Publicado y comentado en mrhonner.com.

La razón áurea como fracción continua en un gif animado de 1ucasvb. Una imagen vale más que mil palabras, sobre todo cuando se mueve:

Infografía práctica para obtener las transformadas rápidas de Fourier, que calculan la transformada de Fourier discreta (DFT) y su inversa, de utilidad para ingenieros.
Pueden visualizarse animaciones de series de Fourier en el fotomat de hoy.
Clic en la imagen abre la imagen entera en la web de Tektronix, empresa que ha realizado la infografía.
Esta entrada participa en la Edición 4.1 del Carnaval de Matemáticas cuyo anfitrión es Tito Eliatron Dixit.