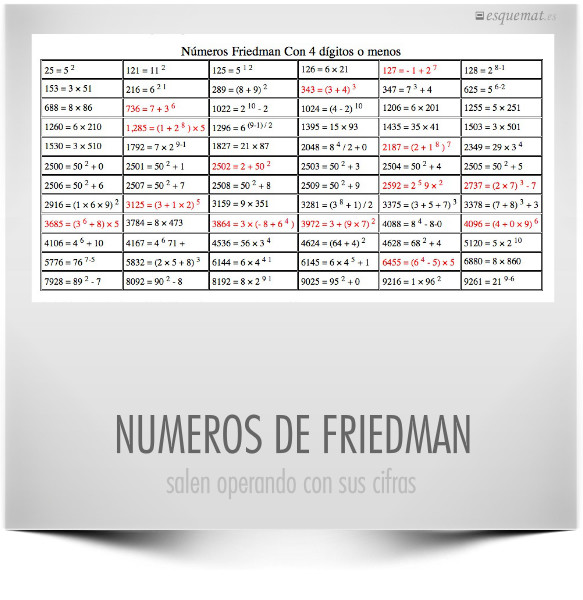
Un número Friedman es un número entero positivo que puede ser escrita de alguna manera no trivial utilizando sus propios dígitos, junto con los símbolos + – × / ^ () y concatenación. Por ejemplo, 25 = 5 2 y 126 = 21 × 6.
El profesor Erich Friedman presenta una tremenda página sobre estos números.
Son muy interesantes para desafiar a los alumnos a encontrarlos, dejando de empujarles a estudiar matemáticas y lanzándoles a hacer matemáticas.
Archivo de la etiqueta: operaciones
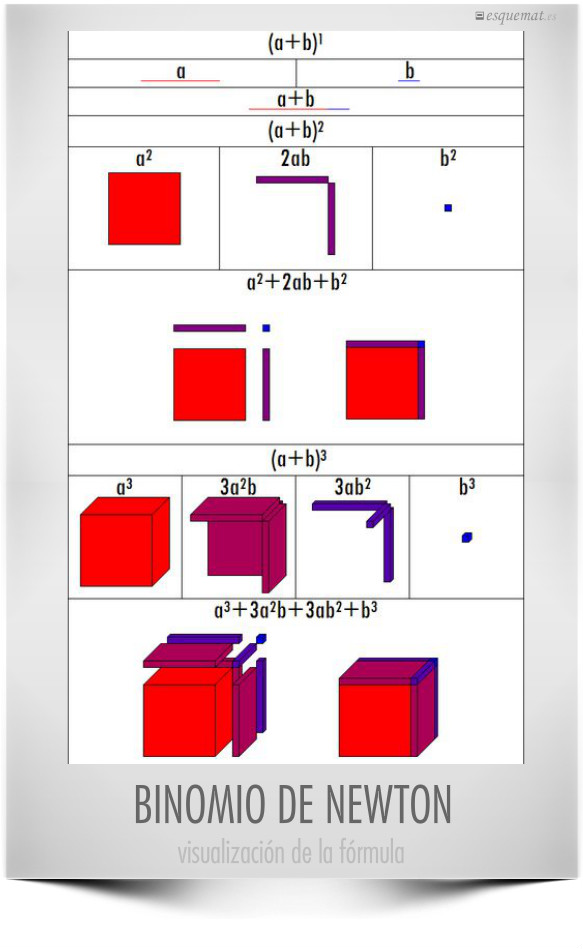
Ya es habitual representar gráficamente la fórmula del cuadrado de una suma (a+b)²=a²+2ab+b² y el autor de do-math da un paso más y nos dibuja la fórmula del binomio de Newton de grado 3. ¿Quien se atreve con la de 4º grado?

Porque se pueden hacer mates sin números. El razonamiento y la acción es como en el sudoku, pero usando bolas de colores. Es el colorku. Lo explica whatdowedoallday y lo vende amazon.
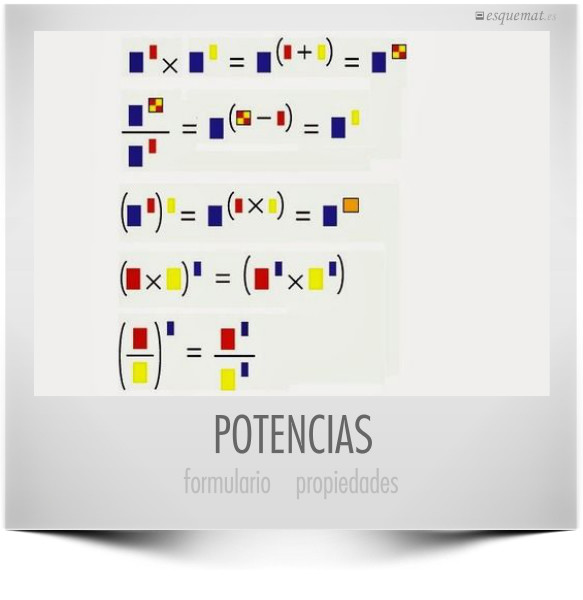
El profesor Alexandre Edigley se atreve a presentar las propiedades de las potencias de un modo original, sustituyendo las variables por colores e ilustrando con ellos sumas y productos. Una idea que puede servir para los que les cueste abstraerse de las letras habituales en el lenguaje algebraico.
Los colores quedan vistosos y recuerdan al extraordinario libro de Euclides ilustrado por Oliver Byrne en 1847.
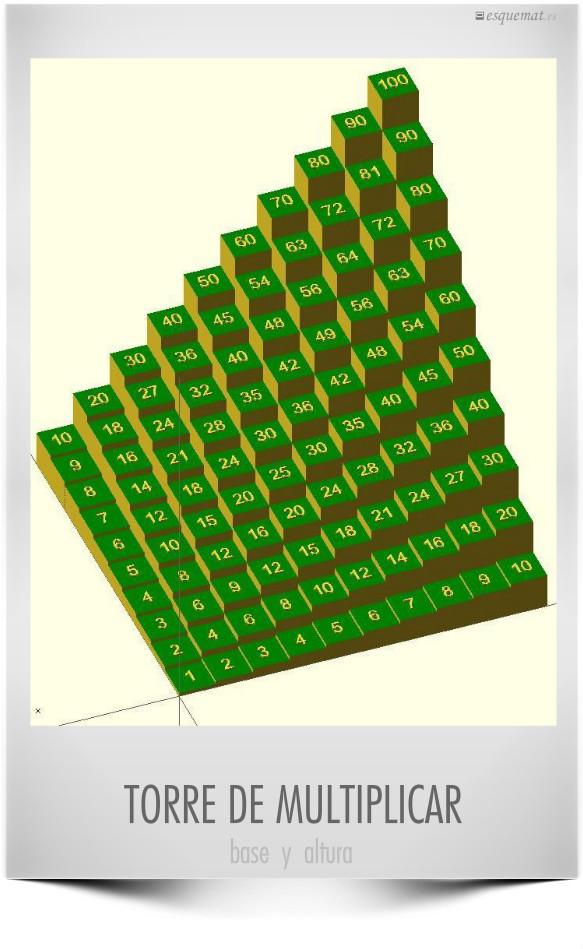
Curiosa e interesante representación 3D de una tabla de multiplicar: cuanto más alto sea el valor más arriba aparece. Original de Roman Hegglin, este tipo de torres de multiplicación se está experimentando con éxito entre los niños, que se plantean buenas preguntas, según nos cuentan y muestran en moebiusnoodles.

Si a algunos les parecen difíciles las operaciones actuales, que se las imagine con este sistema de numeración. Así resolvían problemas de números, fracciones, operaciones y áreas y resulta interesante conocerlo y ver la lógica de su escritura. Infografía de mathsfact, vía Cristina Mier pinterest.

Las curiosidades de los números, siempre fascinantes. Para motivar y animar a descubrir y hacer matemáticas.
De la revista Archives, sobre escritura y arte.

Un documento histórico, de hace 400 años. La multiplicación no cambia, sólo el diseño y la forma de escribir han cambiado. Original de Galileo Galilei (1564-1642).
Enviado por @SilviaP313. Muchas gracias.

Un diseño de Karel Martens que integra el símbolo 5 con su concepto ●●●●● en cinco piezas además color y formas que pueden utilizarse para diseñar otras cifras. En un día en que celebramos una suma que se multiplica por 5.
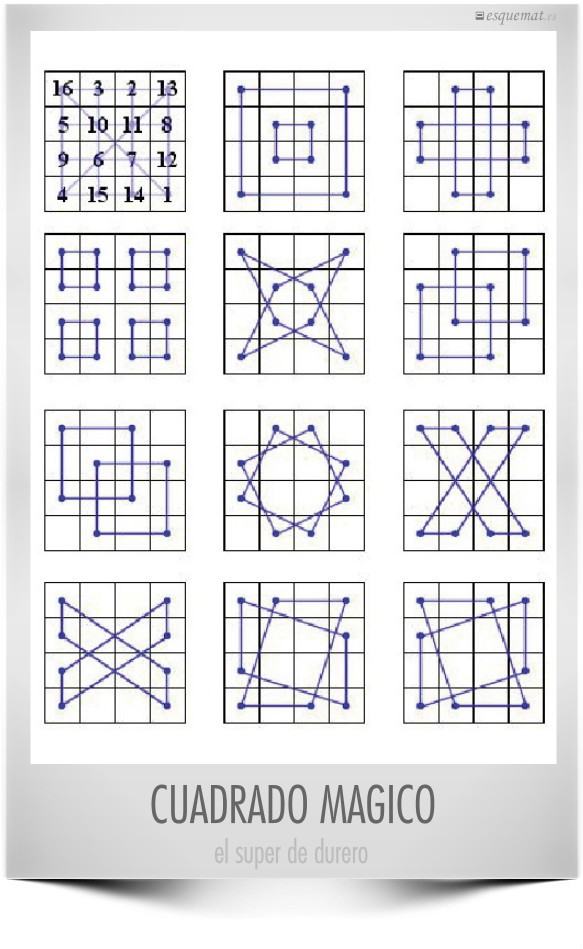
En el cuadrado supermágico de Durero las filas, las columnas y las diagonales suman 34 Pero también los vértices, los números del centro y así hasta las 34 líneas de 4 números de la imagen superior, publicada en The Story of Mathematics. Y hay más sumas que dan 34. De ahí que llamen supermágico al cuadrado de Durero. Todo un artista.
Y más de 34 34’s encuentra, ilustra y comenta @gaussianos en El cuadrado mágico del pintor y acaba proponiendo analizar los cuadrados con los cuadrados y los cubos de los números del de Durero, Y enriquece el tema en La gran belleza de los cuadrados mágicos aportando otros 14 de diversos tamaños y hasta de letras y figuras.
Por su parte @druizaguilera reivindica al escultor Josep Mª Subirachs como autor del cuadrado mágico en la catedral de Gaudí, que admite 310 posibilidades de sumar 33 con 4 casillas, 33 de las cuales podemos ver en el esquemat inferior, con un gráfico del mismo Subirachs. ¡Todo un reto hallar los 310!
Esta entrada participa en la edición 4.1231056 del Carnaval de Matemáticas alojado en Scientia.



