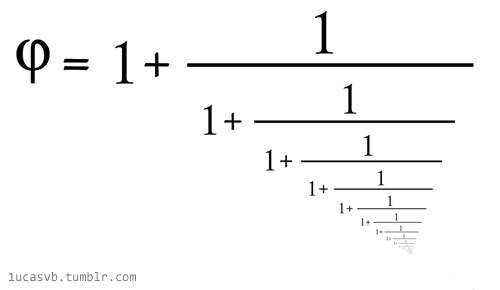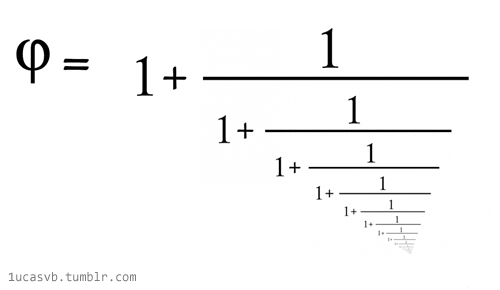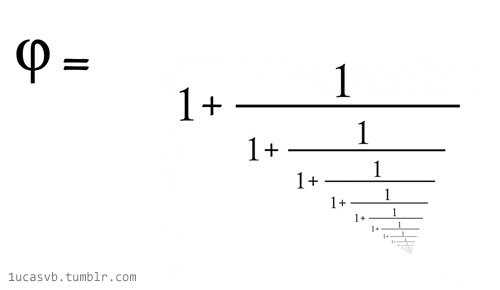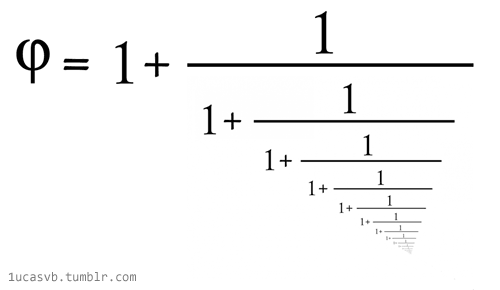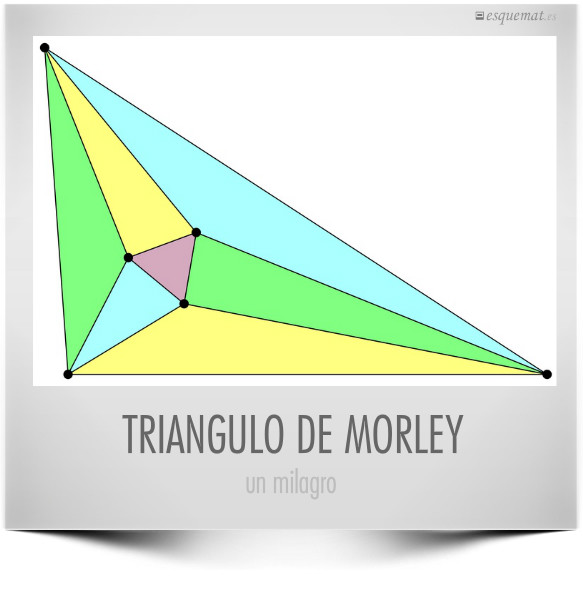
Haciendo la trisección (dividir en 3 partes iguales) de los ángulos de un triángulo se obtiene un triángulo equilátero. Otro milagro de la geometría. Publicado en teorema de Morley.
Archivo de la categoría: proceso
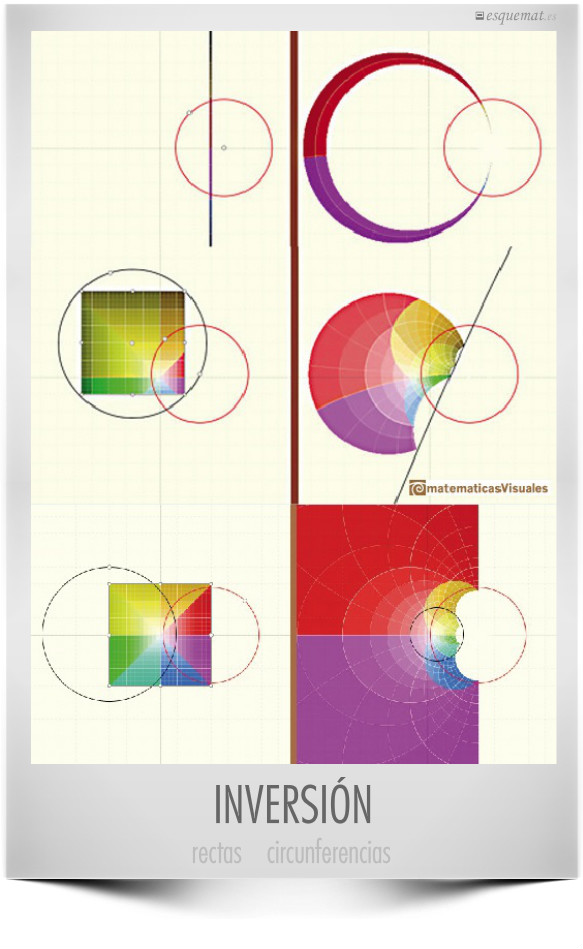
Magníficas ilustraciones sobre la inversión en el plano respecto de una circunferencia en matemáticas visuales.

Del mismo modo que multiplicando por 8 sale una bonita pirámide, al hacerlo por 9 obtenemos esta.
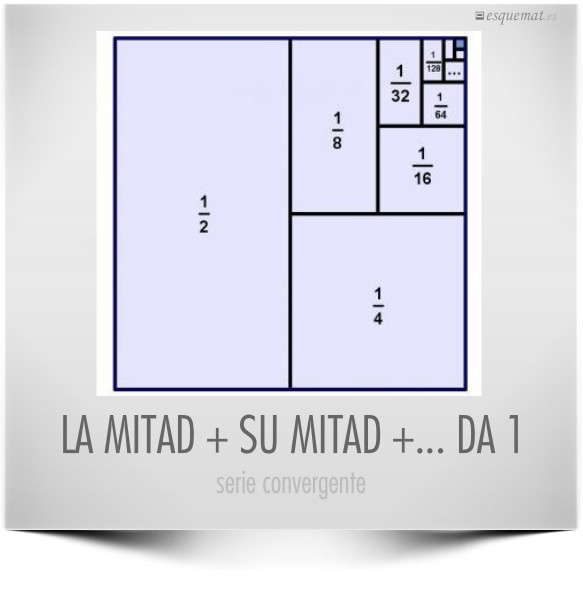
Magnífica demostración visual de que la suma de la serie ½ + ¼ + ¹⁄₈ + ¹⁄₁₆ + … es igual a 1. Porque las cosas no funcionan igual cuando se va al infinito. Publicado y comentado en mrhonner.com.

La relación entre los números del triángulo de Tartaglia y la sucesión de Fibonacci ilustrada claramente. Es bonito y asombroso, pero en realidad en simple, en Fibonacci vamos sumando los dos números anteriores y en Tartaglia hacemos lo mismo de manera un poco más escondida.

La razón áurea como fracción continua en un gif animado de 1ucasvb. Una imagen vale más que mil palabras, sobre todo cuando se mueve:

La suma de números impares consecutivos va dando cuadrados perfectos: 1 + 3 + 5 +…+ (2n-1) = n²
Una interesante fórmula que se demuestra por inducción y que se ve de manera clara y preciosa en este diagrama. Publicado y comentado en la sección visual maths de catonmat.net.

Operaciones que asombran y fascinan y son muy útiles para investigar, buscar regularidades y encontrar propiedades que expliquen resultados tan vistosos como estos. Visto en el pinterest de efonsmaldonado.

Cualquier soporte es bueno para una chuleta de mates, como este paño de cocina Golden Ratio a la venta en zazzle. Colorista y bonito valdría también en versión toalla playera.
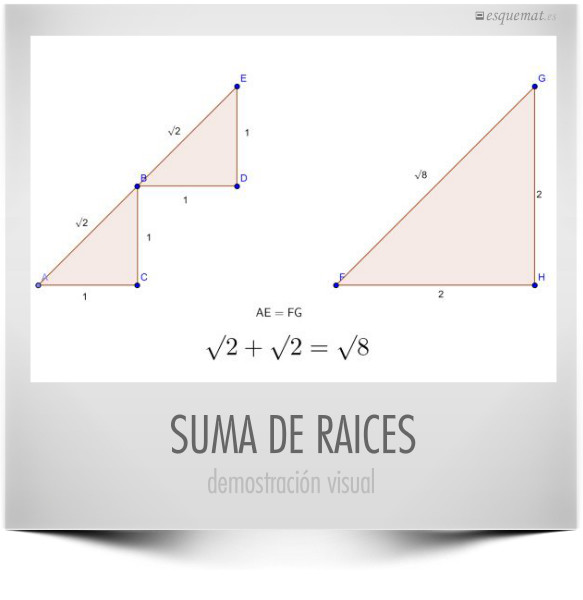
Otra demostración visual simple y contundente, esta vez la prueba de que √2 + √2 = √8.
Imagen, comentarios y otra visión de la misma propiedad en danpearcymaths.