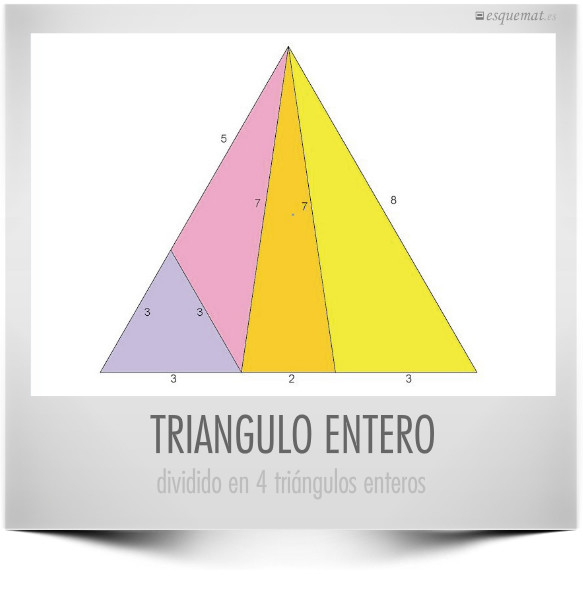
Hoy es día 11 del 12 del 13, 11/12/13, un día apropiado para ver los triángulos equiláteros e isósceles con lados enteros que busca y explica seekecho. Acceso con clic en la imagen.
Archivo de la categoría: proceso
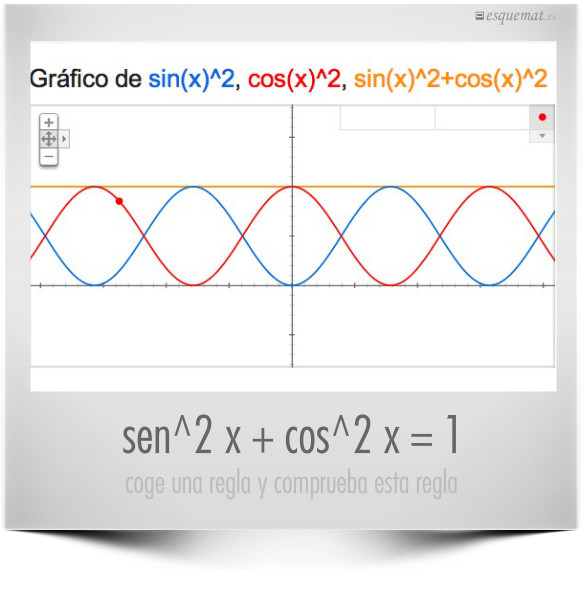
Sabido es que sen² x + cos² x = 1 para cualquier valor de x y aquí tenemos una interesante experiencia para una visión práctica de esta propiedad: Basta ir moviendo una regla a lo largo de las curvas y observar que la altura de la roja y la de la azul van sumando siempre lo mismo, la altura de la recta naranja, que es y = sen² x + cos² x = 1.
La precisión visual es escasa, pero la comprobación puede dejar un poso práctico del asunto.
Las gráficas están realizadas simplemente con google.

Cuando uno ve un logo como el de la Región de Lombardía no se imagina el trabajo de diseño y abstracción que hay detrás. Este esquema sirve tanto para ver la génesis del logo como para reproducirlo en distintos tamaños.
Página del libro ¿Cómo nacen los objetos?
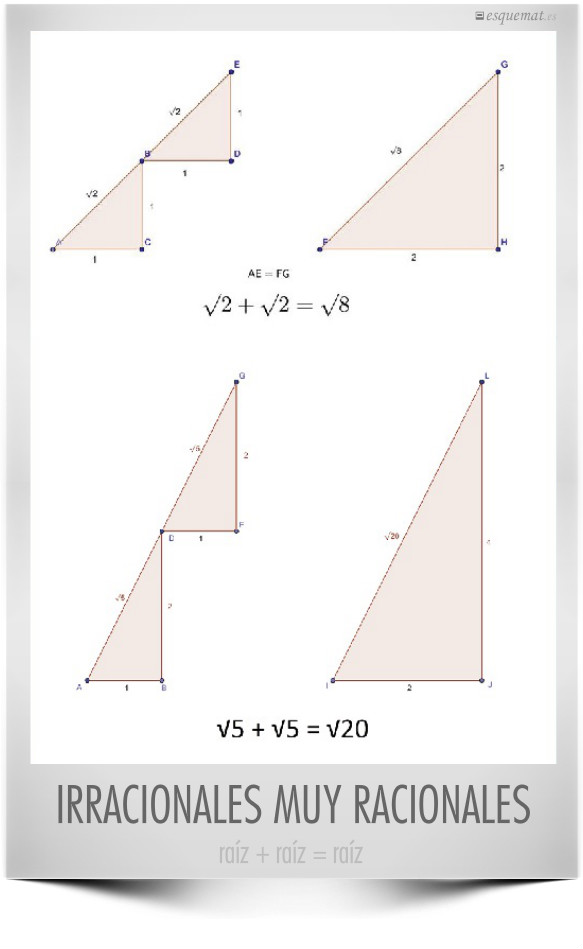
Resulta que al sumar √2 con √2 sale √8 y algo parecido pasa con √5, como se ve claramente dibujando triángulos rectángulos. Los resultados siguen siendo irracionales, pero hay que reconocer que se comportan de manera bastante racional. Y habrá que conformarse con escribir √ delante del número, limitaciones de la técnica.
Está muy bien explicado y ampliado en el mayor semicírculo y algunos irracionales en ecos pitagóricos.
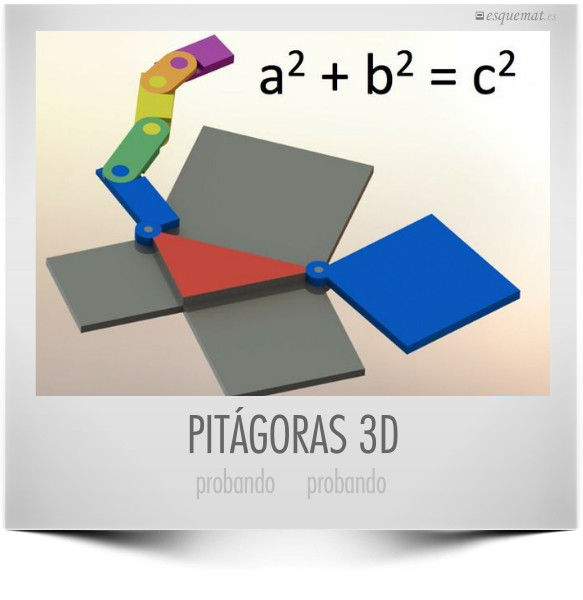
Una visualización, que no demostración, del teorema de Pitágoras, con una interesante conexión con bisagras para mover los cuadrados de los lados y obtener, sumándolos, el cuadrado de la hipotenusa.
Y lo que es mejor, en piezas para imprimir en 3D. The future is now. Otra cosa es tener impresora 3D. The future is tomorrow. Para ver y bajarse gratis en thingiverse.
Esta entrada participa en la edición 4.12310562 del Carnaval de Matemáticas alojado en ::ztfnews.
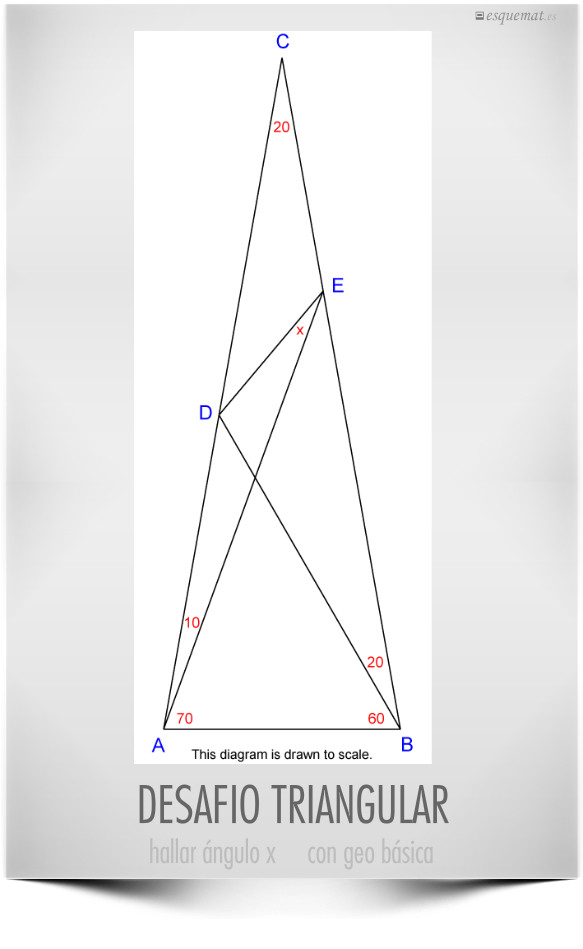
La cosa está en hallar x usando sólo la geometría elemental. Vale que los ángulos de un triángulo suman 180º grados y las propiedades de triángulos semejantes, pero no la trigonometría, seno, coseno, teorema del seno, del coseno y demás.
Cuidado, no ayuda la vista, porque el dibujo no está a escala, y no bastará sumar y restar ángulos, habrá que dibujar más líneas en el interior del triángulo.
Esta entrada participa en la edición 4.12310562 del Carnaval de Matemáticas alojado en ::ztfnews.

Calcular con ecuaciones y dibujar con ordenador es una maravilla. Pero no olvidemos la sencillez y belleza del dibujo manual. Para ver y comprender mejor. Dibujado para sus hijos por la ilustradora Tenney Shawna.

Sencilla y original manera de probar y comprobar áreas, perímetros, raíces, cuadrados, porcentajes. Los psot-it dan mucho de sí. Publicado en E is for Explore, descubierto gracias a Cisca Román.
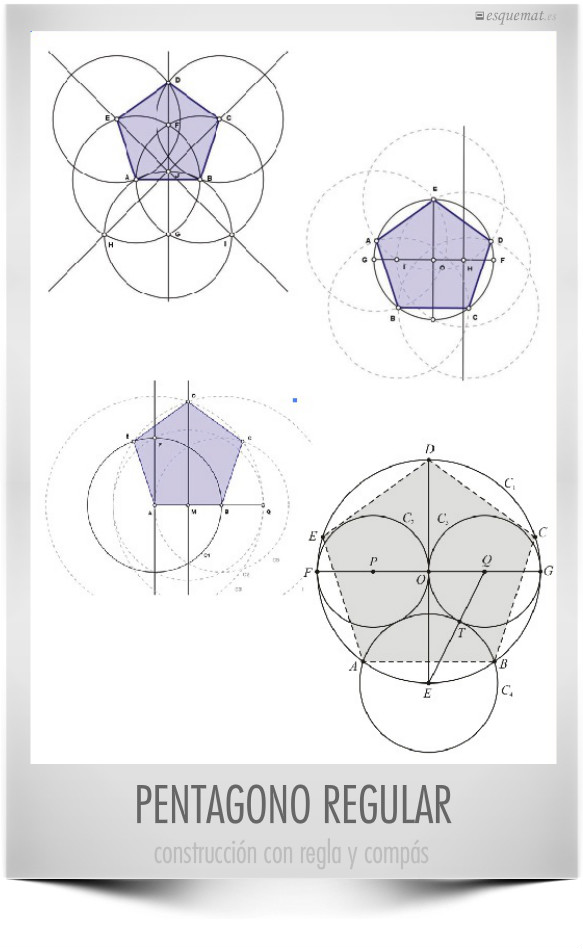
Durante siglos el desafío histórico fue construir la geometría usando solo regla no graduada y compás. Desde O Baricentro da Mente nos muestra Kleber Kilhian hasta 4 métodos para dibujar un pentágono regular con regla y compás. El último, dibujado en gris es el elegante método de Yosifusa Hirano.
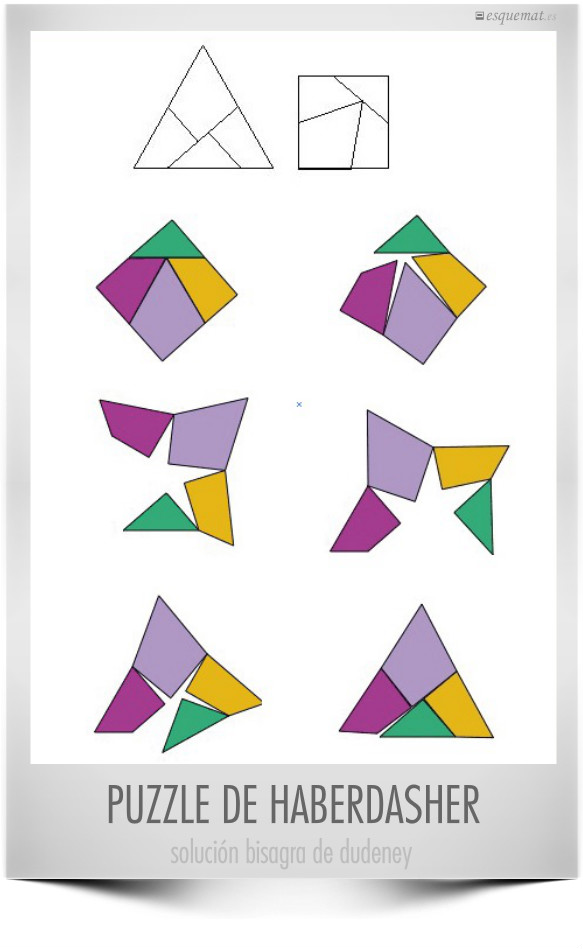
El problema de Haberdasher, cortar un triángulo equilátero en cuatro piezas que formen también un cuadrado, resuelto elegantemente por Henry Dudeney con las piezas unidas por el vértice que, a modo de bisagras, pueden girar para pasar de una figura a la otra.
Expresado en gif animado con código por matthen, inspirado en la versión interactiva de wolframalpha. Espectacular.