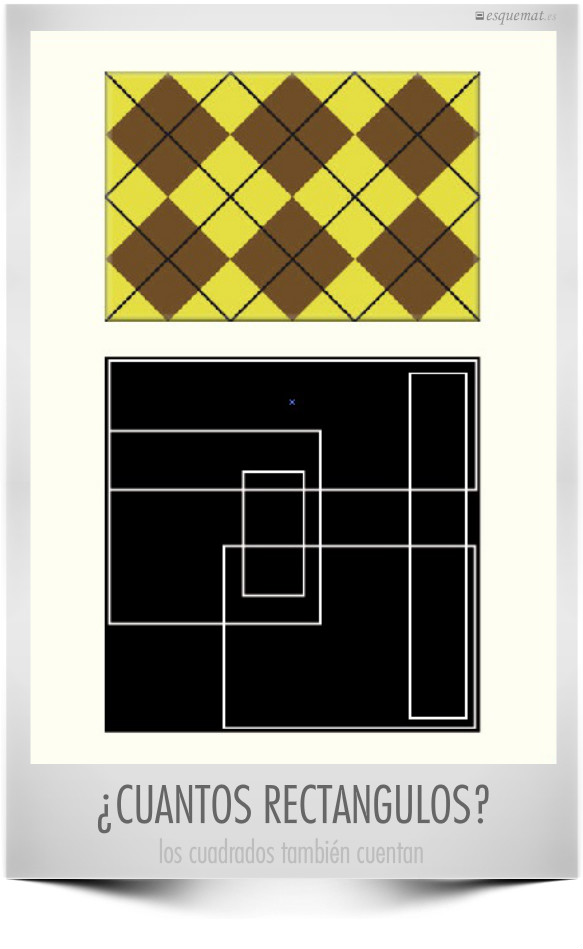
Un problema clásico, que puede plantearse con un fotomat o sobre dibujos geométricos.
Los originales son de transum.org, donde hay una versión pdf, y otras animadas e interactivas.
Clic en la imagen abre el esquemat en pdf.
Archivo de la categoría: _geometría

Composiciones originales inspiradas en la Topología y Topografía. Hay varios, muy hermosos, en surfacearea.org.

Pintamos de rojo un vértice de un cubo, de verde los vértices que están a 1 arista de distancia, de naranja a 2 y de azul a 3. No es la distancia habitual en línea recta, sino la distancia Manhatan, el camino más corto por las aristas. Con los 4 colores tenemos 16 posibilidades que tienen su reflejo en una función booleana que se ve en la imagen. Los colores ilustran la relación entre los 16 números en base 2, de 0000 (0) a 1111 (15) y los vértices seleccionados cada vez en el cubo.
El autor del esquema, Eiichi Wada explica los detalles y la simetría, aunque, eso sí, en japonés.
Esta entrada participa en la edición 4.1231056 del Carnaval de Matemáticas alojado en Scientia.

Uniendo forma y contenido en un hermoso diseño de Waterboy1992.
Esta entrada participa en la edición 4.1231056 del Carnaval de Matemáticas alojado en Scientia.
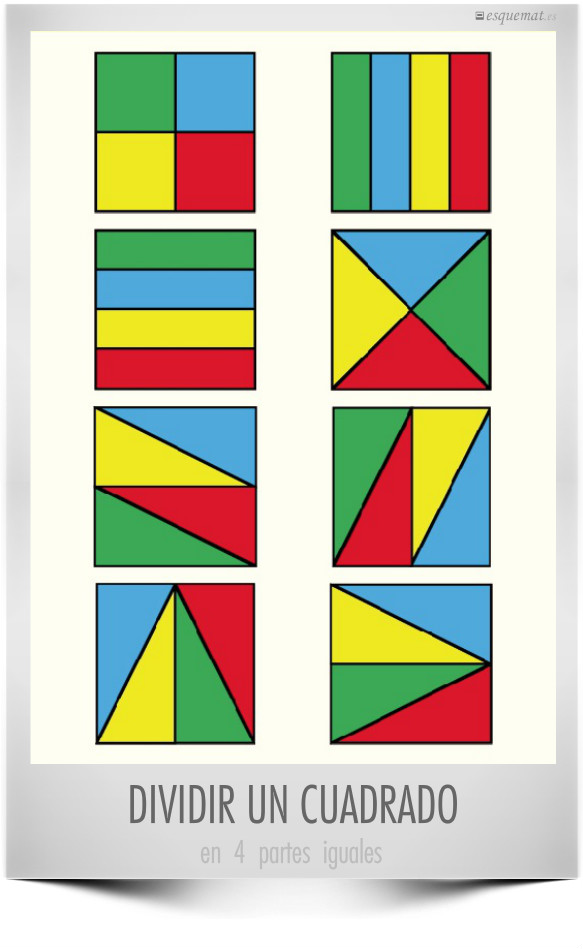
Un ejercicio sencillo para pensar y dejar investigar, dibujar cuadrados y dividirlos en 4 partes iguales. Hay muchas posibilidades y puede hacerse a mano o a máquina, digital, claro. Y se pueden probar otros caso, en 3 partes, en 6, con curvas…
Clic en la imagen abre un pdf con el esquema. Fuente Realm of Maths.
Esta entrada participa en la edición 4.1231056 del Carnaval de Matemáticas alojado en Scientia.

Cualquier método es bueno para ilustrar el Teorema de Pitágoras. Se hace con cuadrados sobre los lados, pero se puede hacer con círculos o piezas de lego o tomates o cualquier figura. La de hoy es muy sabrosa, con crujientes crackers (≈ galletitas): 9 sobre un lado + 16 sobre el otro = 25 en la hipotenusa. ¡Que aproveche! Publicado en el MoMath.
Esta entrada participa en la edición 4.1231056 del Carnaval de Matemáticas alojado en Scientia.

Porque jugar con las figuras y sus posibilidades y buscar formas hermosas también es una actividad creativa y matemática. Variantes de diseño sobre un hexágono, de la mano de Facu Ontivero.

Un retrato de Newton, obra de Eulogia Merle que forma parte de la exposición Libros inmortales, instrumentos esenciales en el MUNCYT de La Coruña, anunciada con una completa galería de retratos de científicos en Sinc.
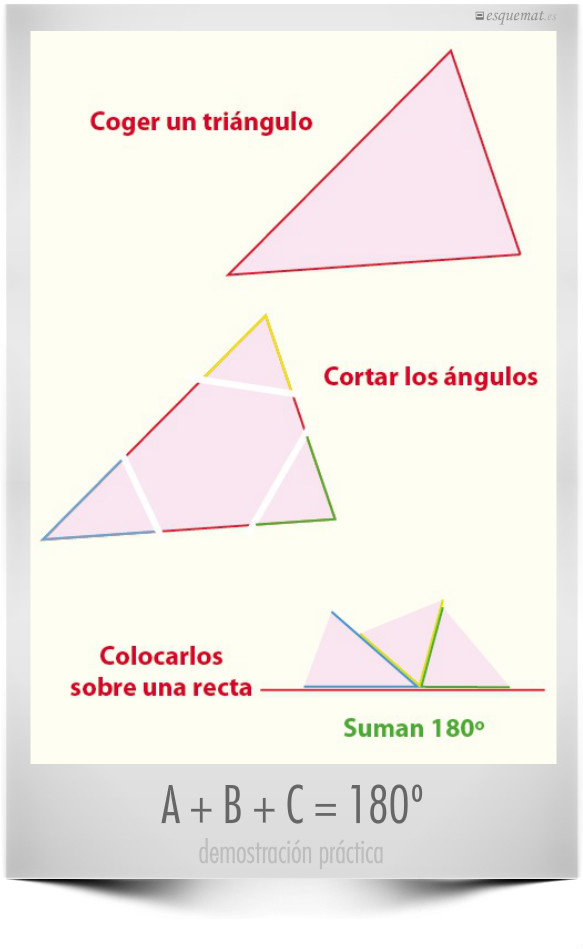
Sencilla y contundente demostración visual de que los 3 ángulos de un triángulo suman 180º. Para todas las edades.
Se puede probar con distintos tipos de triángulos, como se puede ver en learnatmathematicsrealm, fuente de la idea.
Clic en la imagen abre la demo en un pdf tamaño A4.

Un juego increíblemente sencillo, divertido y estimulante para la mente. Se empieza pintando libremente cada hexágono de la fila superior de la plantilla de colores, azul, rojo o amarillo.
Y se sigue, fila a fila, con 2 reglas:
1- Si los dos hexágonos anteriores son del mismo color, el hexágono intermedio de la fila siguiente se pinta de ese color.
2-Si los dos hexágonos anteriores son de distinto color, el hexágono intermedio de la fila siguiente se pinta del tercer color.
Se producen multitud de situaciones distintas y se puede jugar a formar figuras, prever el color del vértice y a mil cosas que explican y muestran en pinkmathematics.
La idea original es de Steve Humble, publicada en el New York Times.
Y @Calaix2 recoge el juego en su Blog del Calix +ie en un detallado y bien ilustrado post y amplía el desafío con distintas opciones y materiales. Ánimo y ¡a jugar!


