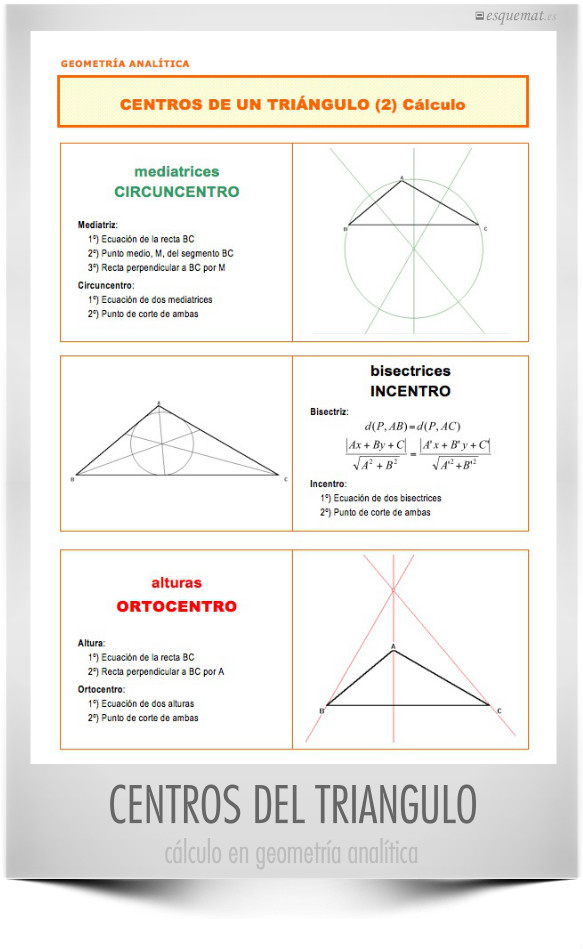
Nombres y gráfica de los centros de un triángulo con indicaciones y fórmulas para encontrar sus coordenadas con ecuaciones de rectas.
Guía:
Clic en la imagen abre el esquema completo de 2 páginas en pdf para ver, descargar o imprimir.
Guía prof:
El es apropiado en geometría analítica, con coordenadas de puntos y ecuaciones de rectas. Para un nivel más sencillo, puede utilizarse los Centros de un triángulo (1) Descripción.
Archivo de la categoría: _geometría
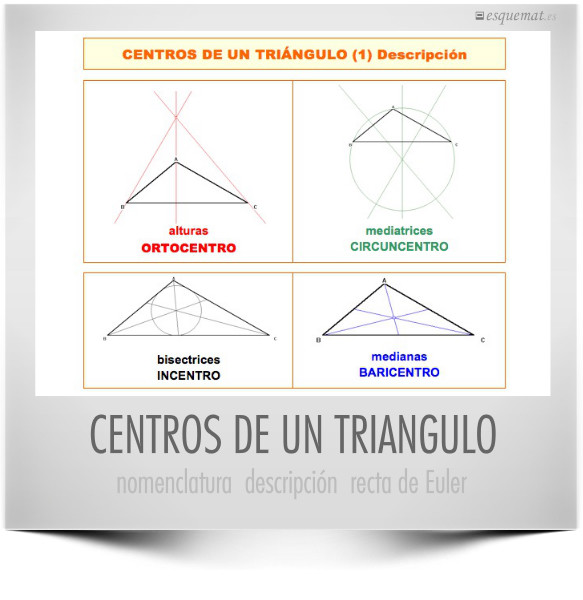
Nomenclatura, definición y gráfica de los centros de un triángulo.
Guía:
Clic en la imagen abre el esquema completo en pdf para ver, descargar o imprimir.
Guía prof:
Este esquema está orientado sólo a conocer los centros, sus nombres y sus propiedades de manera visual: Los centros de las circunferencias inscrita y circunscrita, las distancias del baricentro a los vértices y la recta de Euler: Ortocentro, baricentro y circuncentro siempre están alineados.

Esquemas por niveles con las definiciones a conocer y las propiedades a demostrar en trigonometría, desde ángulos y triángulos hasta la generalización y sus aplicaciones.
Guía:
Clic en la imagen abre el esquema completo en pdf para ver, descargar o imprimir.
Guía prof:
Para poder editar el esquema y adaptarlo al gusto de cada uno puede descargarse en doc en este enlace esquema de trigonometría

La geometría analítica en el espacio, con los conceptos a conocer y los métodos y problemas a resolver. Los vectores se usan de dos maneras, para posiciones en el espacio afín, basado en los puntos, rectas, planos y posiciones, y para productos y medidas en el euclídeo, que añade la media y con ella distancias, ángulos, áreas y volúmenes.
Guía: Se señalan con distintos símbolos los conceptos a definir y las propiedades a demostrar o resolver. El esquema sirve de mapa para situar el conocimiento e ir marcando lo que ya se sabe.
Guía prof: Es efectivo separar el estudio del espacio afín, y el espacio euclídeo
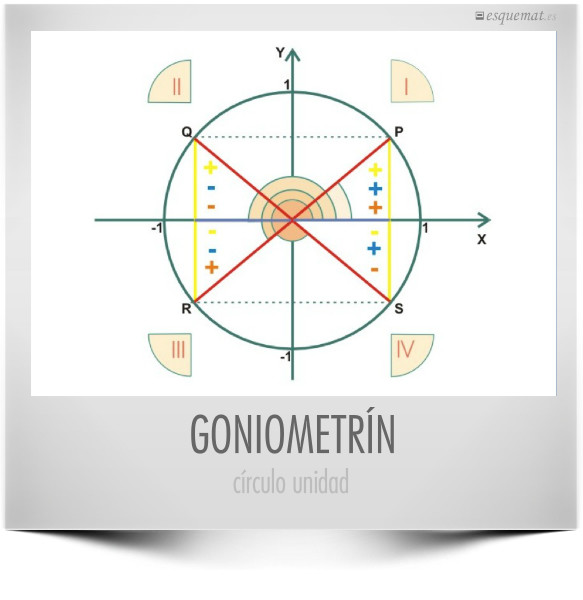
La circunferencia goniométrica permite situar en los ejes de coordenadas los ángulos y sus razones trigonométricas. Este dibujo sirve para reducir al 1º cuadrante los ángulos de los cuatro cuadrantes.
Guía:
Ayuda mucho tener siempre delante este dibujo cuando se trabaja con trigonometría.
Los cuadrantes se numeran con I, II, III y IV y en cada uno de ellos aparecen el segmento y el signo del seno y el coseno. También está el signo de la tangente, pero no su segmento, que estaría fuera de la circunferencia y que no hay que confundir con el radio que vale siempre 1.
Guía prof:
Clic en la imagen abre un pdf con goniometrines de 6×6 y 9×9 cm para imprimir en cartulina y repartir a los alumnos. El uso de términos desenfadados y poco formales quita aspereza a las Mats y llamarle goniometrín triunfa siempre entre los jóvenes.
Resulta más útil e instructivo relacionar las razones trigonométricas de los distintos cuadrantes por medio de la visión geométrica y la comprensión del significado que memorizando un montón de fórmulas del tipo sen (180+α)= −sen α