Construyendo cuadrados sobre los lados de un triángulo rectángulo en un proceso reiterado se obtiene un árbol de Pitágoras, un fractal que toma diversas formas según sea el triángulo inicial. El de la figura, muy bien resuelto, llega al orden 8 y alcanza bastante más en el gif animado original de scipsy:
Árbol de Pitágoras de scipsy
Sobre una sencilla rejilla de un rectángulo con sus diagonales se forman las letras de este póster de Henryk Stazewski para una exposición en Polonia. Una idea interesante para potenciar la visión geométrica, creatividad y diseño de formas y fuentes y utilizarlo de paso para chuletas y presentaciones de geometría.
No se puede hacer la tierra plana, sin hacer grietas en ella, pero sí proyectarla en distintas formas, señalan en New Scientist. Jack van Wijk de la Universidad Tecnológica de Eindhoven, en los Países Bajos, utiliza algoritmos para cortar y desarrollar la superficie de la Tierra, minimizando la distorsión, en una proyección myriahedral. Muy interesante para motivar y experimentar en el aula.
Desarrollo, enlaces y otros mapas en bldgblog. Y más en dymaxion map:
Dymaxion map
Una sencilla visualización de las curvas que aparecen al seccionar un cono, publicada junto a la historia y usos en la vida real de la parábola en parabolaonline. Son las cónicas.
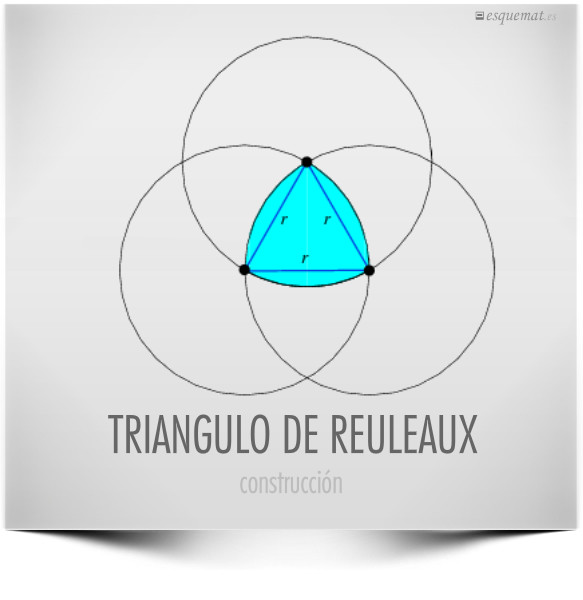
Proceso para construir un triángulo de Reuleaux con regla y compás a partir de un triángulo equilátero. Publicado en allofthemath, puede verse un precioso post con construcciones y ejemplos en images.math.cnrs.fr y un superpost de mati y sus aventuras.
Diseño basado en las figuras planas básicas, triángulo, cuadrado, círculo y circunferencia. Muy sugerente, puede servir como póster o ilustración en apuntes y presentaciones.
Obra de Eugen Batz, que estudia el efecto espacial de los colores y formas al estilo Kandinsky en la Bauhaus Dessau,1929.
Vivimos en 3 dimensiones y no nos cabe como podrían ser otras superiores. Pero podemos imaginarnos como sombras 3D de un mundo 4D.
Descansando hoy de ideas y razones traemos una decoración geométrica de ISO50Blog. Hay muchos artistas y sitios dedicados a la geometría visual que podemos usar para ilustrar y decorar, porque también en matemáticas hay un tiempo para empaparse de belleza y armonía y dejar fluir intuición y visualización.
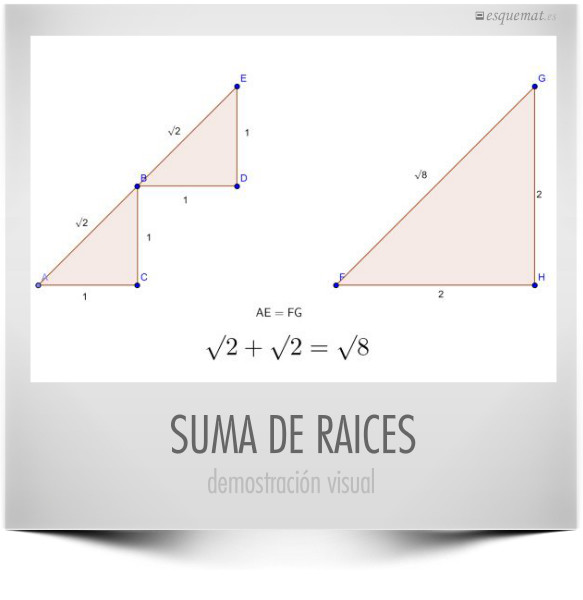
Otra demostración visual simple y contundente, esta vez la prueba de que √2 + √2 = √8.
Imagen, comentarios y otra visión de la misma propiedad en danpearcymaths.
