
Si una función de una variable tiene una gráfica en el espacio, las de 2 variables las tienen en el espacio, lo que es más difícil de visualizar y dibujar. Para ello se puede usar google, también wolframalpha o un generador de gráficas 3D, pero Eric M. Thompson lo ha realizado papel y plegable. ¡Muy bueno!.
Archivo de la categoría: _cálculo
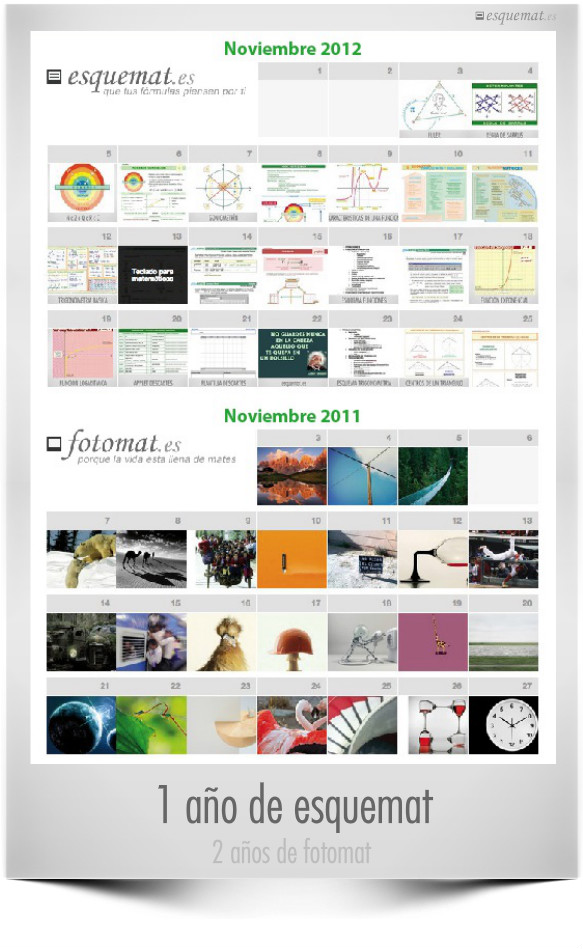
Hoy se cumple 1 año desde el 1º esquemat, 365 intentos de no llevar en la cabeza lo que quepa en el bolsillo, de dejar que las fórmulas trabajen por ti. Y hoy se cumplen 2 años de fotomat, mirando la vida con los ojos llenos de mates. Y en la vocación de facilitar la comprensión de las mates lo celebramos invitando a visitar los calendarios con los 730 fotomat y los 365 esquemat. Gracias a todos los que apoyan y animan estos proyectos.
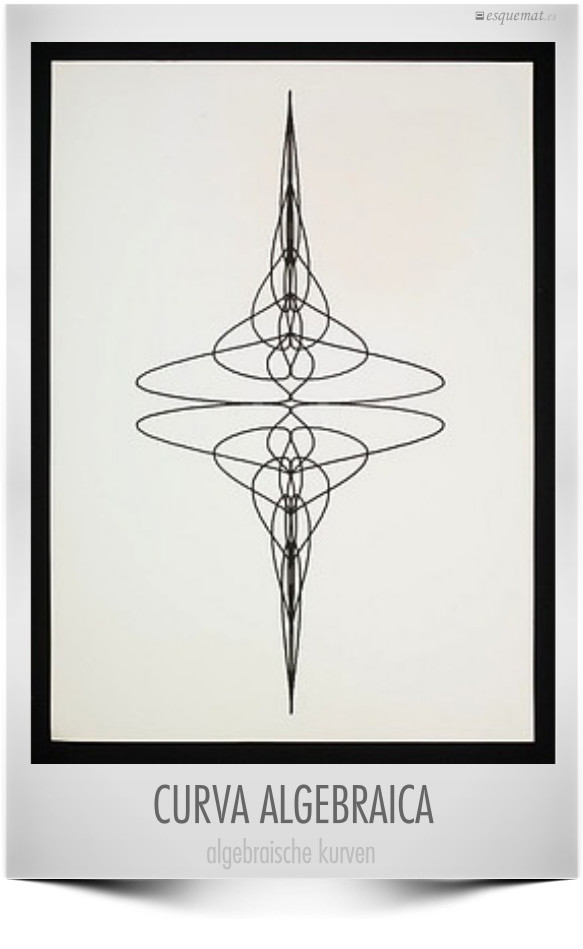
También conviene a veces parar de razonar y simplemente contemplar. Hay mucho arte de base geométrica, el de hoy es una curva algebraica en una serigrafía diseñada por el artista Herbert W. Franke y el programador Peter Henne.

Pintamos de rojo un vértice de un cubo, de verde los vértices que están a 1 arista de distancia, de naranja a 2 y de azul a 3. No es la distancia habitual en línea recta, sino la distancia Manhatan, el camino más corto por las aristas. Con los 4 colores tenemos 16 posibilidades que tienen su reflejo en una función booleana que se ve en la imagen. Los colores ilustran la relación entre los 16 números en base 2, de 0000 (0) a 1111 (15) y los vértices seleccionados cada vez en el cubo.
El autor del esquema, Eiichi Wada explica los detalles y la simetría, aunque, eso sí, en japonés.
Esta entrada participa en la edición 4.1231056 del Carnaval de Matemáticas alojado en Scientia.
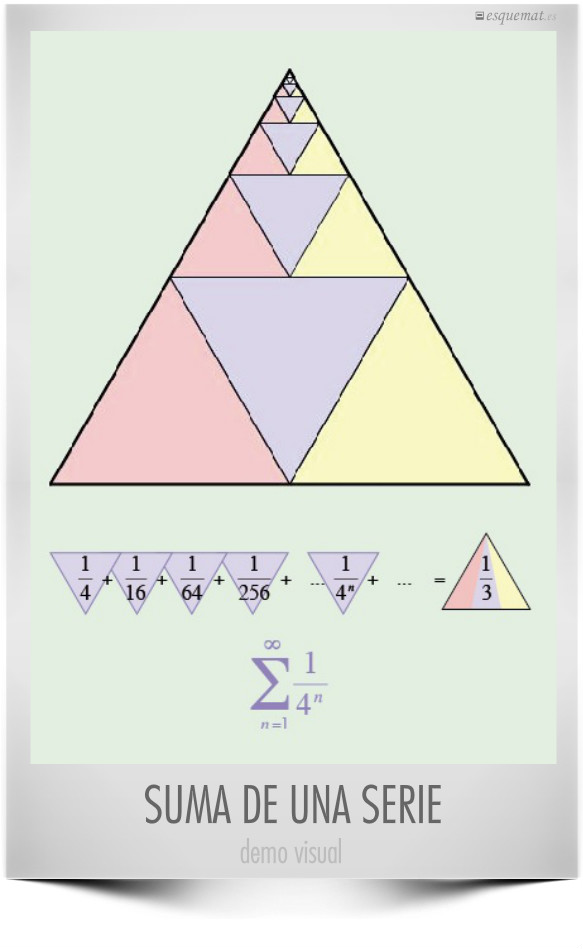
Visualización de la suma de la serie infinita de los inversos de las potencias de 4. La dejamos sin palabras, para que cada uno trate de comprenderlo.
La explicación detallada está en mrhonner.com, publicada el 11/11/11, que llama día del triángulo equilátero, por tener 3 números iguales.
Clic en la imagen abre un pdf con el esquema en A4.
Esta entrada participa en la edición 4.1231056 del Carnaval de Matemáticas alojado en Scientia.

Un retrato de Newton, obra de Eulogia Merle que forma parte de la exposición Libros inmortales, instrumentos esenciales en el MUNCYT de La Coruña, anunciada con una completa galería de retratos de científicos en Sinc.

El símbolo integral ∫ es una estilización del que indica la suma, el sumatorio ∑, porque La integral da el resultado de una suma infinita. Y así lo han visto, integrando infinitos colores en uno, en el icono de la App Calculus X.

Una forma práctica de recomendar recursos web de cualquier tema. Un marcapáginas que en este caso lleva por una cara una selección de sitios web generales, imposible poner los muchos buenos que hay, y por la otra mis sitios web con su definición y enlaces.
Clic en la imagen abre un pdf en A4 con 2 páginas, que permiten imprimir 6 marcapáginas de 7 x 14’85 cm. Recomendado usar impresora en color con la cartulina más gruesa que admita. Aunque si se van a plastificar basta imprimir sobre un folio normal, mejor de 100 gr.
Con esta plantilla en word se pueden personalizar los marcapáginas copiando y pegando logos y direcciones en las celdas de las tablas. Permite sacar marcapágs. especiales para cada tema, materia, trimestre… realizados por el profe o por los alumnos de cada grupo, que aprenden de paso técnicas de edición.
Esta entrada participa en la edición 4.123105 del Carnaval de Matemáticas en Cifras y Teclas.
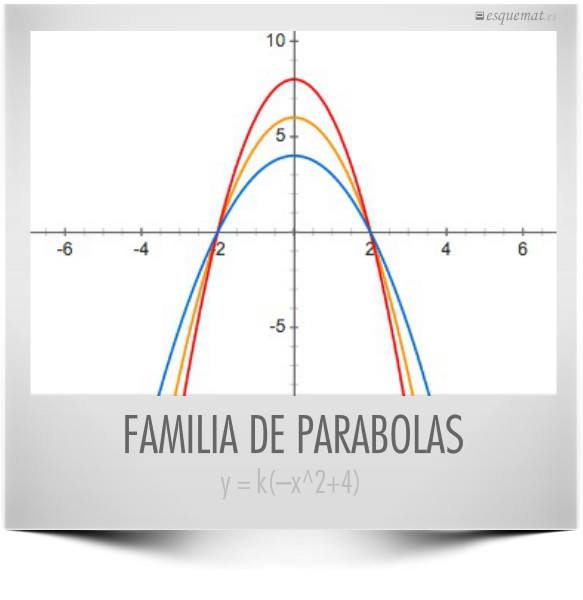
Podemos dibujar cualquier parábola y = ax² + bx +c que corte a los ejes y dibujarla después multiplicando su expresión por cualquier número y = k(ax² + bx +c). Obtendremos una familia de parábolas que cortan a los ejes en los mismos puntos. La del gráfico está hecha escribiendo en google y=-x^2+4, y=2*(-x^2+4), y=1.5*(-x^2+4) y hay una visión más poética en el fotomat de hoy.
Esta entrada participa en la edición 4.123105 del Carnaval de Matemáticas en Cifras y Teclas.

Con unas pocas líneas de código en Mathematica, Andrea publica en trulydiscombobulated esta visualización de una suma de Riemann en 3 dimensiones. Muy claro para comprender la integral.
Esta entrada participa en la edición 4.123105 del Carnaval de Matemáticas en Cifras y Teclas.


