Archivo de la categoría: _álgebra

Publicado el por
Responder

APRENDER CON EL EJEMPLO
WolframAlpha.com es el extraordinario generador de resultados basado en el motor de Mathematica. Devuelve datos y resultados de mates y de cualquier cosa, como muestran en su página de ejemplos, mejor y más directa que un largo y tedioso manual de uso.
Y en una nueva prueba de imaginación y dinamismo wα presenta en su página de inicio (de la versión de ordenador, en mobile no sale) cientos de iconos enlazados a búsquedas particulares sobre distintos temas. Para no perdérselo.

Publicado el por
Responder

APERTURA DEL DIFRAGMA
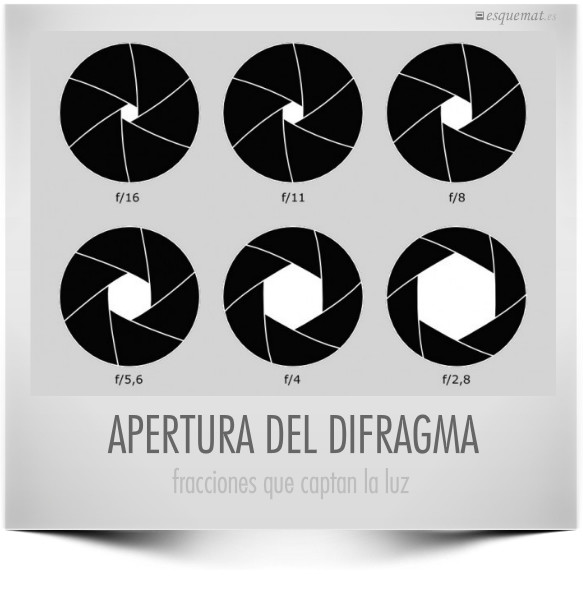
Un doble recurso para aprender fotografía y mostrar un uso práctico de las fracciones, áreas, distancias y cuadrados, todo muy bien ilustrado y explicado en el blog de Martin Opladen.

Publicado el por
4

NUMEROS COMPLEJOS
Póster del conjunto de los números Complejos que destaca el símbolo C con el que se denota el conjunto, indica las operaciones posibles, muestra los ejes con los números reales como componentes y ejemplos de representación de complejos como vectores, con un guiño en los colores que indica que contiene a los naturales, los enteros, los racionales y los reales y expone de manera concisa su definición como un par ordenado de números reales.
Diseño original de @notemates para esquemat.es: Versión imagen sin marco. Versión pdf A4.
Entrada para la Edición 4.1231 del Carnaval de Matemáticas en el blog i-matemáticas.com de JGM.

Publicado el por
4

NUMEROS REALES
Póster del conjunto de los números Reales que destaca el símbolo R con el que se denota el conjunto, indica las operaciones posibles, muestra como ejemplo algunos números de distintos tipos, en particular π, e y Φ, con un guiño en los colores que indica que contiene a los naturales, los enteros y los racionales, y expone de manera concisa su definición axiomática y los nombres de otras formas de construcción de este conjunto.
Diseño original de @notemates para esquemat.es: Versión imagen sin marco. Versión pdf A4.
Entrada para la Edición 4.1231 del Carnaval de Matemáticas en el blog i-matemáticas.com de JGM.

Publicado el por
9

NUMEROS RACIONALES
Póster del conjunto de los números Racionales que destaca el símbolo Q con el que se denota el conjunto, indica las operaciones posibles, muestra como ejemplo algunos números de distintos tipos, decimales y fraccionarios, con un guiño en los colores que indica que contiene a los naturales y a los enteros, y expone de manera concisa su definición como conjunto cociente de una relación de equivalencia entre pares de números enteros, en el que el segundo término no es 0.
Diseño original de @notemates para esquemat.es: Versión imagen sin marco. Versión pdf A4.
Entrada para la Edición 4.1231 del Carnaval de Matemáticas en el blog i-matemáticas.com de JGM.

Publicado el por
12

NUMEROS ENTEROS
Póster del conjunto de los números Enteros que destaca el símbolo Z con el que se denota el conjunto, indica las operaciones posibles, muestra como ejemplo los primeros números positivos y negativos, con un guiño en los colores que indica que contiene a los naturales, y expone de manera concisa su definición como conjunto cociente de una relación de equivalencia entre pares de números naturales.
Diseño original de @notemates para esquemat.es. Versión imagen sin marco. Versión pdf A4.
Entrada para la Edición 4.1231 del Carnaval de Matemáticas en el blog i-matemáticas.com de JGM.

Publicado el por
14

NUMEROS NATURALES
Póster del conjunto de los números INaturales que destaca el símbolo IN con el que se denota el conjunto, indica las operaciones posibles, muestra como ejemplo los primeros números y expone de manera divulgativa, no rigurosa, los Axiomas de Peano con que se definen.
Diseño original de @notemates para esquemat.es: Versión imagen sin marco. Versión pdf A4.
Entrada para la Edición 4.1231 del Carnaval de Matemáticas en el blog i-matemáticas.com de JGM.

Publicado el por
Responder

SER O NO SER
To be or not to be. El problema es ser o su complementario, no ser, y la unión con el complementario es el todo, así que ser ∪ no ser = todo. Un divertido ejemplo de uso del lenguaje matemático para promocionar obras literarias.
El diseñador gráfico Nicholas Weltyk expresa en posters de 12″x18″ tres obras de Shakespeare
ilustrando con gráficos matemáticos citas  de Romeo y Julieta, Hamlet y El sueño de una noche de verano. Shakespeare in Math.

Publicado el por
Responder

EL SISTEMA SOLAR

Publicado el por
1

FIBONACCI A LA VISTA
Se extienden las matemáticas visuales: esquemas, diagramas y dibujos que muestran y demuestran conceptos y propiedades. Como esta visualización, alegre y clara, de los primeros términos de la sucesión de Fibonacci publicada en geometric-aesthetic, blog de estética geométrica.
Nos gusta Fibonacci.