Archivo de la categoría: _aplicaciones

Publicado el por
3

CUADRADO MAGICO
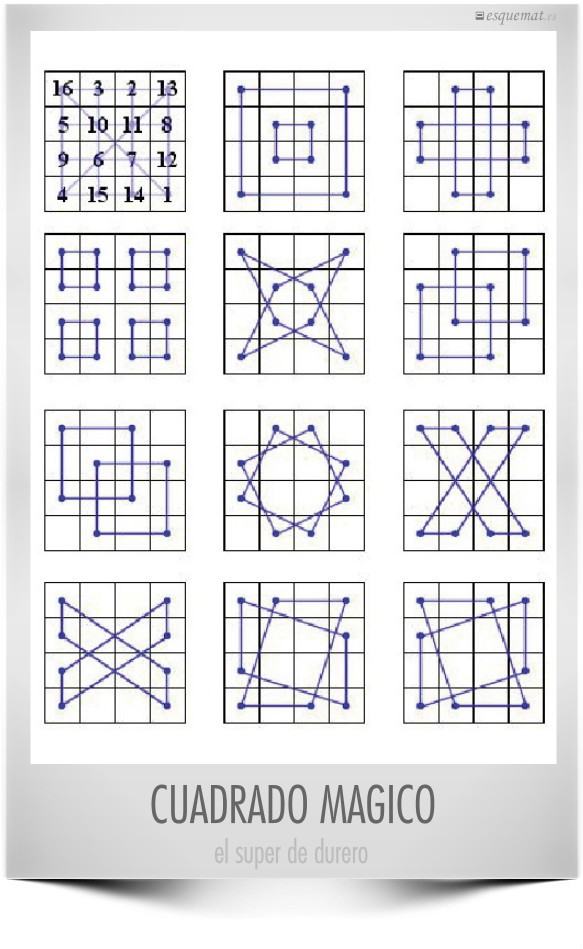
En el cuadrado supermágico de Durero las filas, las columnas y las diagonales suman 34 Pero también los vértices, los números del centro y así hasta las 34 líneas de 4 números de la imagen superior, publicada en The Story of Mathematics. Y hay más sumas que dan 34. De ahí que llamen supermágico al cuadrado de Durero. Todo un artista.
Y más de 34 34’s encuentra, ilustra y comenta @gaussianos en El cuadrado mágico del pintor y acaba proponiendo analizar los cuadrados con los cuadrados y los cubos de los números del de Durero, Y enriquece el tema en La gran belleza de los cuadrados mágicos aportando otros 14 de diversos tamaños y hasta de letras y figuras.
Por su parte @druizaguilera reivindica al escultor Josep Mª Subirachs como autor del cuadrado mágico en la catedral de Gaudí, que admite 310 posibilidades de sumar 33 con 4 casillas, 33 de las cuales podemos ver en el esquemat inferior, con un gráfico del mismo Subirachs. ¡Todo un reto hallar los 310!
Esta entrada participa en la edición 4.1231056 del Carnaval de Matemáticas alojado en Scientia.

CUADRADO MAGICO EN BCN

Publicado el por
1

CODIGO MORSE
Con dos elementos, si/no, 0-1, punto/raya puede decirse todo. Así con impulsos eléctricos corto/largo nació el alfabeto morse que abrió el camino a las comunicaciones actuales.

PERSPECTIVAS
Porque jugar con las figuras y sus posibilidades y buscar formas hermosas también es una actividad creativa y matemática. Variantes de diseño sobre un hexágono, de la mano de Facu Ontivero.

ISAAC NEWTON
Un retrato de Newton, obra de Eulogia Merle que forma parte de la exposición Libros inmortales, instrumentos esenciales en el MUNCYT de La Coruña, anunciada con una completa galería de retratos de científicos en Sinc.

ONDAS GRAVITATORIAS
Un científico dijo “No puedo demostrar esta fórmula, pero es tan bonita que tiene que ser correcta”. Hay una profunda belleza y armonía en el conocimiento de las cosas, como en estas ondas gravitatorias producidas por dos agujeros negros en órbita. La búsqueda de estas ondas trata de hacer visible lo invisible y corroborar su existencia, que la teoría de la relatividad general de Einstein pronosticó hace 100 años.

MILLION YEAR CALENDAR
Un calendario que sirve para 1 millón de años y más. Basta girar las piezas cada mes para tenerlo siempre al día. Con 7 piezas de madera lacada de ciprés, obra de Keita Shimizu, a la venta en Japón por ￥9,345.
Aunque, como siempre, lo más interesante es descubrir uno mismo cómo hay que poner los números para que la cosa funcione. Y compararlo con el calendario perpetuo del MOMA.

MATES A HUEVO
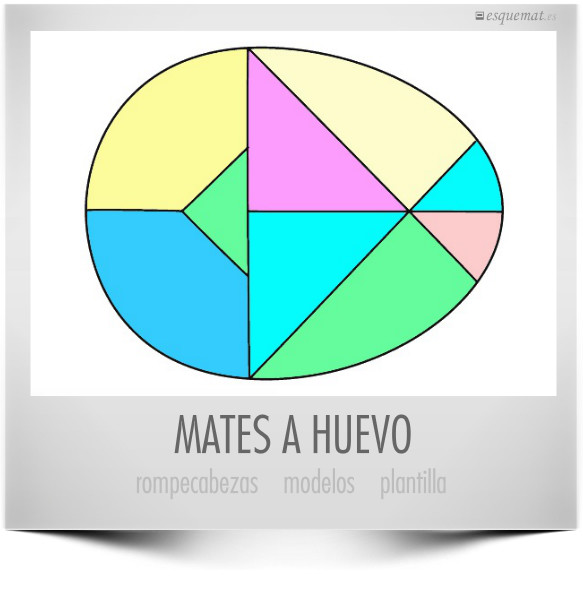
Ingredientes: Modelo ovoide con partición de colores y plantilla imprimible para recortar las piezas.
Receta: Imprimir la plantilla, colorear (opcional), a mano o digital,  y recortar las piezas.
Modo de empleo: Repartir las piezas y tratar de formar, usándolas todas, las aves publicadas en nrich.maths y que se encuentran también en el doc BirdsToMake. Al terminar hay que formar de nuevo el huevo sin mirar el despiece.
Es una variante del tangram.

GEOMETRY POSTERS
El gusto por la geometría entra por los ojos. Y por el trazado de figuras. Sirvan de inspiración los  pósters geométricos de Amanda Rohlin.
AMANDA ROHLIN
POSTERS GEOMETRICOS

Publicado el por
1

MATCAPAGINAS WEB
Una forma práctica de recomendar recursos web de cualquier tema. Un marcapáginas que en este caso lleva por una cara una selección de sitios web generales, imposible poner los muchos buenos que hay, y por la otra mis sitios web con su definición y enlaces.
Clic en la imagen abre un pdf en A4 con 2 páginas, que permiten imprimir 6 marcapáginas de 7 x 14’85 cm. Recomendado usar impresora en color con la cartulina más gruesa que admita. Aunque si se van a plastificar basta imprimir sobre un folio normal, mejor de 100 gr.
Con esta plantilla en word se pueden personalizar los marcapáginas copiando y pegando logos y direcciones en las celdas de las tablas. Permite sacar marcapágs. especiales para cada tema, materia, trimestre… realizados por el profe o por los alumnos de cada grupo, que aprenden de paso técnicas de edición.
Esta entrada participa en la edición 4.123105 del Carnaval de Matemáticas en Cifras y Teclas.

Publicado el por
1

RELOJ CMYK
Tres discos traslúcidos con los colores básicos Cian, Magenta, Yellow giran al compás del tiempo. El menor marca las horas, el mediano los minutos, el pequeño los segundos, y los tres juntos dan a cada momento una variedad de colores. Porque con tres colores se obtienen todos los demás, como la base de un espacio vectorial. Y porque cada momento es único y se puede medir sin números. Obra original de Louie Rigano, que tiene otra versión con triángulos:

Esta entrada participa en la edición 4.123105 del Carnaval de Matemáticas en Cifras y Teclas.