Porque se pueden hacer mates sin números. El razonamiento y la acción es como en el sudoku, pero usando bolas de colores. Es el colorku. Lo explica whatdowedoallday y lo vende amazon.
Responder
Archivo del Autor: notemates
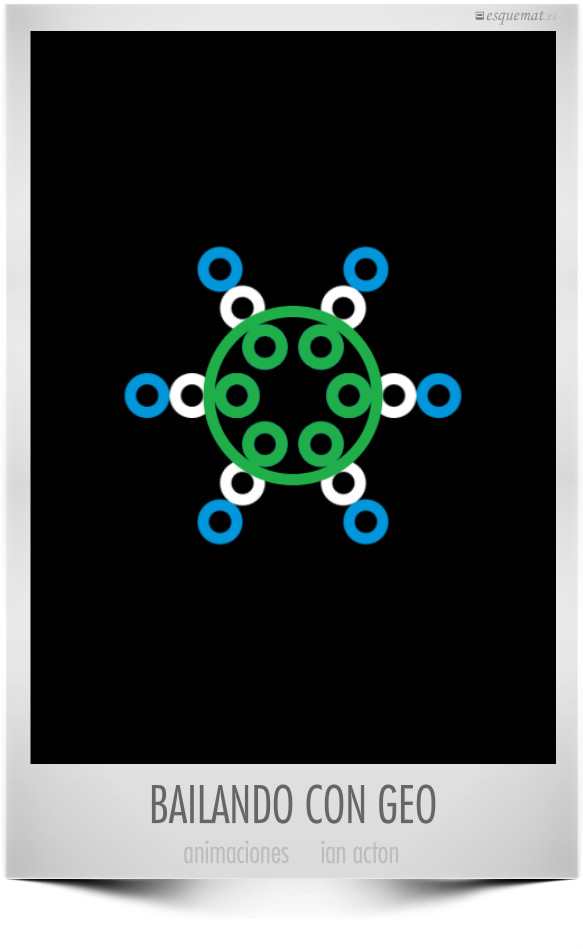
Con simples figuras básicas y buena imaginación y ritmo el animador inglés Ian Acton realiza varias series tituladas Geometric Gifs Animated. Es bonito e hipnotizante y satisface el gusto intuitivo por la armonía de las formas geométricas. Hay muchos y variados, vemos aquí uno de ellos:
Geometría que baila en la edición 5.1 del Carnaval de Matemáticas en titoeliatrondixit.
Los esquemas ya no son lo que eran. Uno empieza con esquemas de mates y no para de encontrar ideas dinámicas. En Minute Labs han realizado un espectacular generador de patrones que localizan e ilustran la posición de los números primos, de fibonacci, primos de fibonacci, sumas de fibonacci, de carmichael, ternas pitagóricas… y hasta al azar o con el término general que se quiera de cualquier sucesión. Y salen, a elegir, en cuadrícula, espiral de Ullam, de Vogel, en triángulo o pirámide y con el color y zoom que se desse. Todo en Number Constellations. Impresionante.
Nubes de números en la constelación de la edición 5.1 del Carnaval de Matemáticas en titoeliatrondixit.
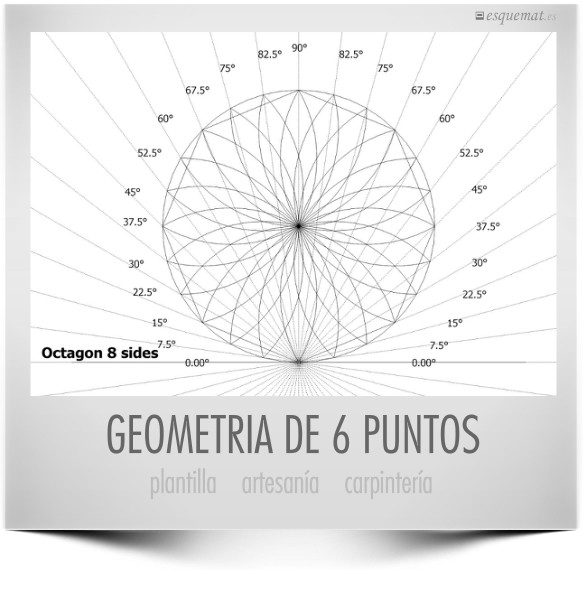
Dividiendo una circunferencia en 48 partes tenemos una plantilla sobre la que se pueden dibujar polígonos regulares de 3, 4, 6, 8, 12, 16, 24 y 48 lados. El matemático persa del siglo X Abul Wafa al-Buzjani escribió el tratado Sobre las partes de Geometría Necesarias para Artesanos sobre la geometría de 6 puntos y otros tipos que pueden verse en las alfombras persas y en la geometría de margarita de los albañiles y carpinteros medievales.
Y el carpintero y constructor americano Sim Ayers presenta estas plantillas y otros fascinantes dibujos de geometría práctica para la realización de arcos, vigas y techos en su Roof Framing Geometry.
Esta entrada participa en la edición 5.1 del Carnaval de Matemáticas en titoeliatrondixit.
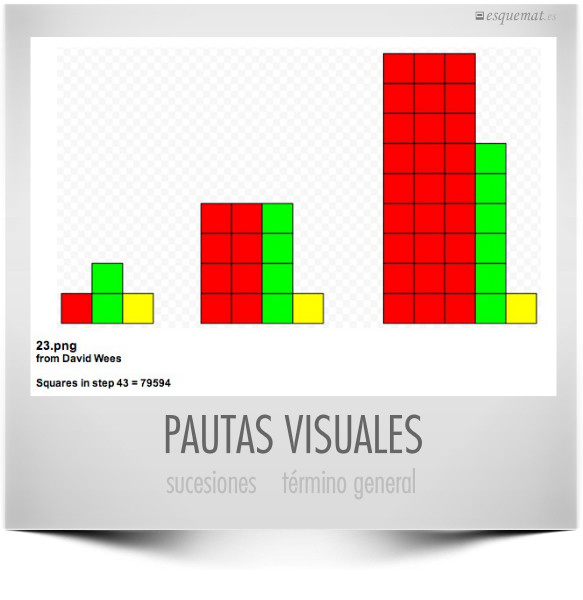
Te muestran los 3 primeros elementos de una sucesión y te dicen el valor del 43º desafiándote a deducir la expresión del término general. Y así hasta 140 veces en visualpatterns, un magnífico sitio de álgebra visual donde profesores y alumnos proponen las pruebas. Para divertirse, razonar y aprender. Por cierto la sucesión de la imagen es… a„ = n³ + 2n + 1 ← selecciona con el ratón.
Descubierto gracias a microsiervos.
Post que participa en la edición 5.1 del Carnaval de Matemáticas en titoeliatrondixit.
Y ¿cual será la solución de este otro?:
Otra experiencia matemática y artística original del diseñador gráfico Marcos Gonyea que puede animar a realizar experimentos similares. Requiere contar de 1 a 100 formando imágenes, figuras y simetrías en un trabajo sistemático, metódico y ordenado. Puras mates.
Estos pixeles participan en la edición 5.1 del Carnaval de Matemáticas en titoeliatrondixit.
Un mismo punto puede ser vértice de varios polígonos que lo rodean completamente. El blog de Don Steward nos muestra varios casos y nos invita a reflexionar sobre si otros son posibles no.
Esta entrada participa en la edición 5.1 del Carnaval de Matemáticas en titoeliatrondixit.
“ Si no lo puedes explicar de manera sencilla, no lo entiendes bien del todo”
dice Albert Einstein
” No entiendes bien una cosa si no puedes explicarselo a tu abuela”
También lo dijo Einstein
Pues eso, hagámoslo simple y claro, que demasiado rollo confuso hay en el mundo. En lo que podamos y en lo demás mejor que hable el que que sabe.
Entrada ∊ edición 5.1 ∊ Carnaval de Matemáticas ⊂ titoeliatrondixit.
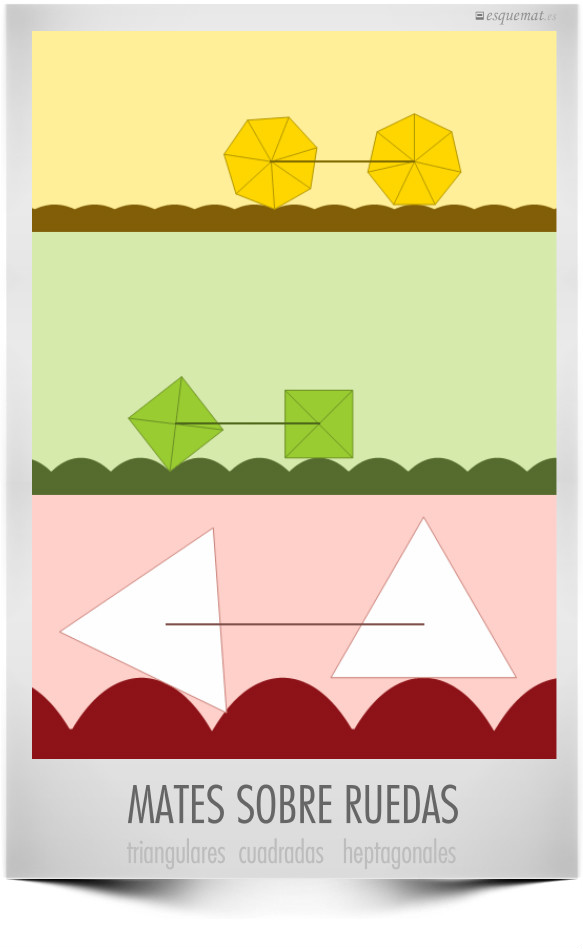
Las ruedas suelen redondas, lo que viene muy bien con un suelo plano. pero también hay quien se atreve a probar con ruedas cuadradas, adaptando el suelo con la curva catenaria conveniente. Un diseño animado por movies and math y hecho realidad en el MoMath, con un efecto mágico que no nos cansamos de ver:
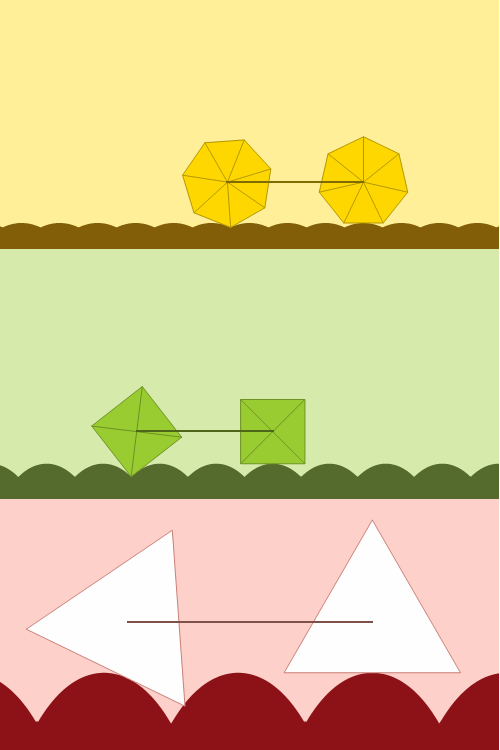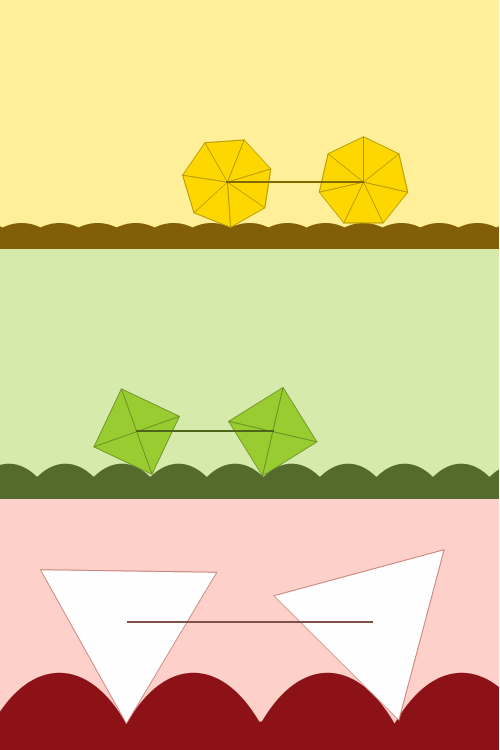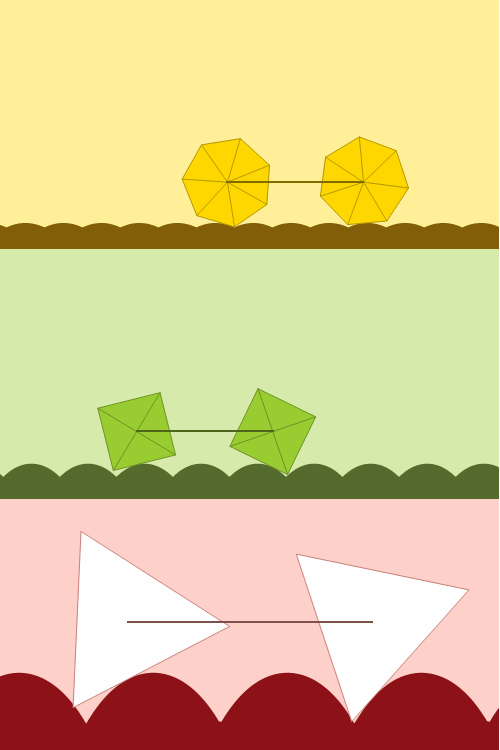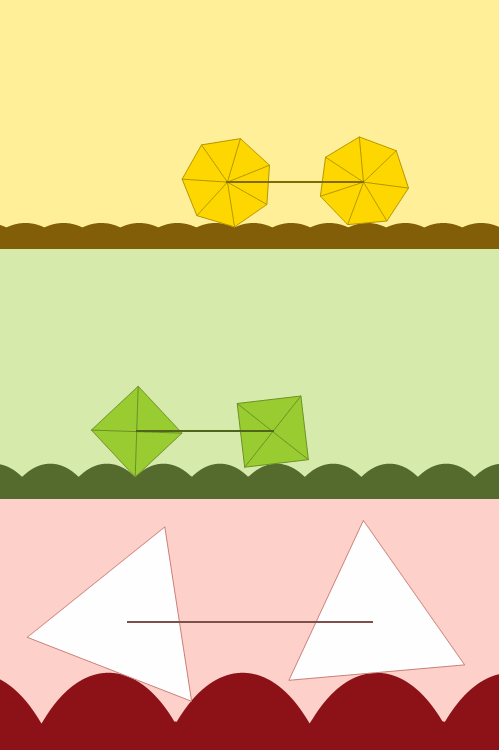Esta entrada participa en la edición 5.1 del Carnaval de Matemáticas alojado en titoeliatrondixit.
Usando en cada caso las mismas 7 piezas del tangram podemos formar estas 3 copas, pero una está completa y las otras tienen huecos diferentes. La vista engaña, pero la geometría no. ¿Qué es lo que ocurre?. Podemos resolverlo saboreando un tangranwich.
Sam Lloyd presentó esta paradoja en su libro Eighth Book of Tan de 1903. Imagen de wikipedia.
