Hoy nos vamos por lo artístico con un póster de Andrew Bird que ilustra montañas con polígonos y espirales. Porque la geometría es bella.
Responder
Archivos Mensuales: agosto 2013
Construyendo cuadrados sobre los lados de un triángulo rectángulo en un proceso reiterado se obtiene un árbol de Pitágoras, un fractal que toma diversas formas según sea el triángulo inicial. El de la figura, muy bien resuelto, llega al orden 8 y alcanza bastante más en el gif animado original de scipsy:
Árbol de Pitágoras de scipsy
¿De qué color es el cielo? Depende del lugar, la fecha y la hora. I love Charts nos ofrece este esquema que resume y simplifica la inmensa infografía contínua de IAmNoTreeIAmAnEnt con fotos de los colores del cielo a lo largo de un día. Un esquema simple, directo, claro, coloredo, genial.
Sobre una sencilla rejilla de un rectángulo con sus diagonales se forman las letras de este póster de Henryk Stazewski para una exposición en Polonia. Una idea interesante para potenciar la visión geométrica, creatividad y diseño de formas y fuentes y utilizarlo de paso para chuletas y presentaciones de geometría.
Publicado en 9GAG
Del mismo modo que multiplicando por 8 sale una bonita pirámide, al hacerlo por 9 obtenemos esta.
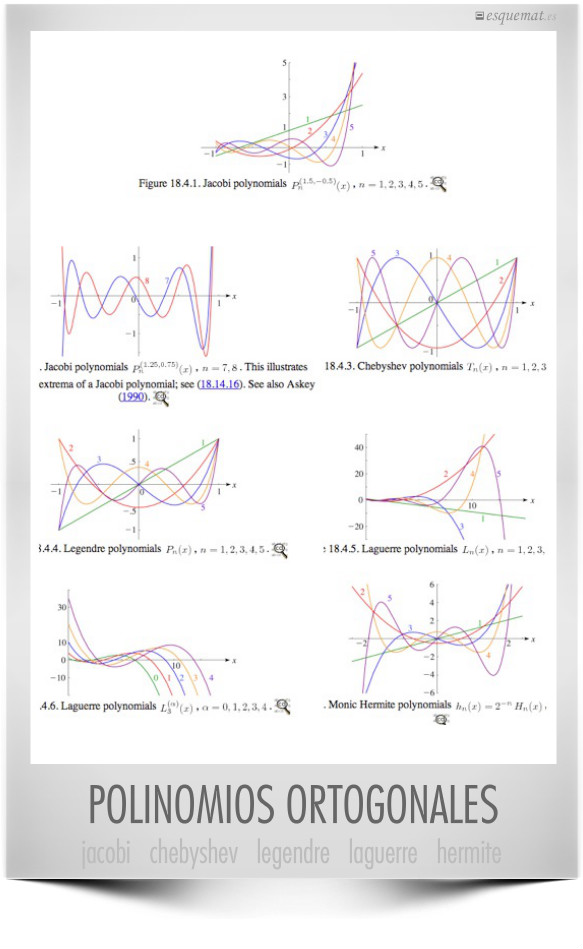
Una muestra de algunos casos de polinomios ortogonales. Puede usarse como referencia al estudiarlos, pero también para mostrar en cursos básicos para despertar curiosidades y hacer ver que hay un mundo más allá de lo elemental.
Se encuentran perfectamente definidos y desarrollados en la Digital Library of Mathematical Functions.
Y con un puntito poético tenemos hoy un fotomat de Chebysev.
No se puede hacer la tierra plana, sin hacer grietas en ella, pero sí proyectarla en distintas formas, señalan en New Scientist. Jack van Wijk de la Universidad Tecnológica de Eindhoven, en los Países Bajos, utiliza algoritmos para cortar y desarrollar la superficie de la Tierra, minimizando la distorsión, en una proyección myriahedral. Muy interesante para motivar y experimentar en el aula.
Desarrollo, enlaces y otros mapas en bldgblog. Y más en dymaxion map:
Dymaxion map
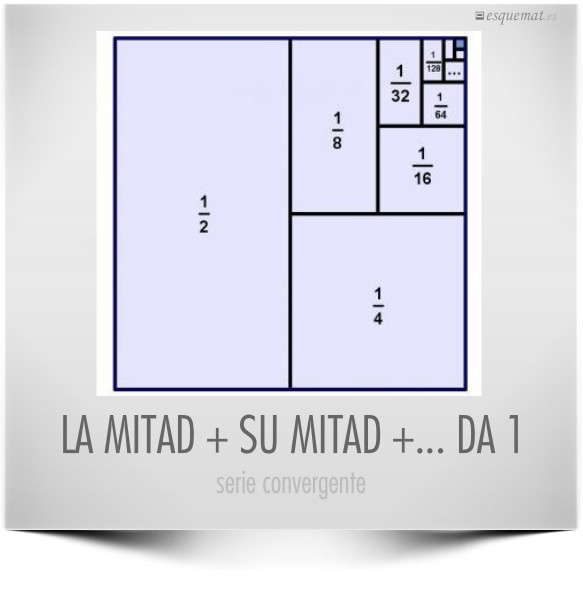
Magnífica demostración visual de que la suma de la serie ½ + ¼ + ¹⁄₈ + ¹⁄₁₆ + … es igual a 1. Porque las cosas no funcionan igual cuando se va al infinito. Publicado y comentado en mrhonner.com.
Una segunda entrega de los pósters de Jennifer Farley dedicados a la física, en este caso con dos cilindros concéntricos y una referencia a las coordenadas cilíndricas.
