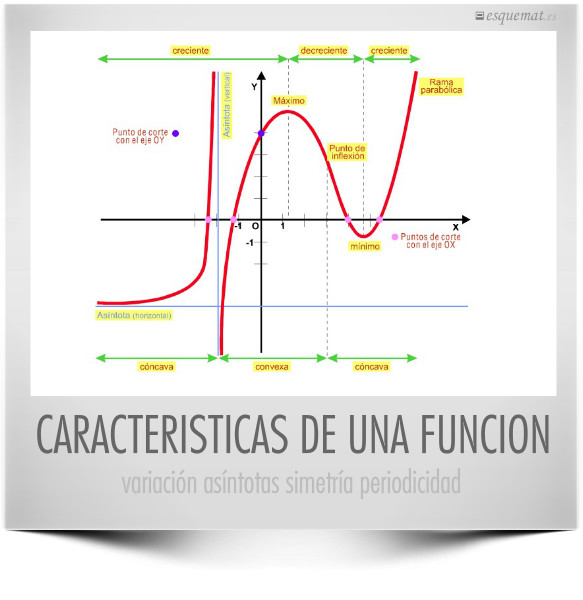
La geometría analítica en el espacio, con los conceptos a conocer y los métodos y problemas a resolver. Los vectores se usan de dos maneras, para posiciones en el espacio afín, basado en los puntos, rectas, planos y posiciones, y para productos y medidas en el euclídeo, que añade la media y con ella distancias, ángulos, áreas y volúmenes.
Guía: Se señalan con distintos símbolos los conceptos a definir y las propiedades a demostrar o resolver. El esquema sirve de mapa para situar el conocimiento e ir marcando lo que ya se sabe.
Guía prof: Es efectivo separar el estudio del espacio afín, y el espacio euclídeo
Archivos Mensuales: noviembre 2012
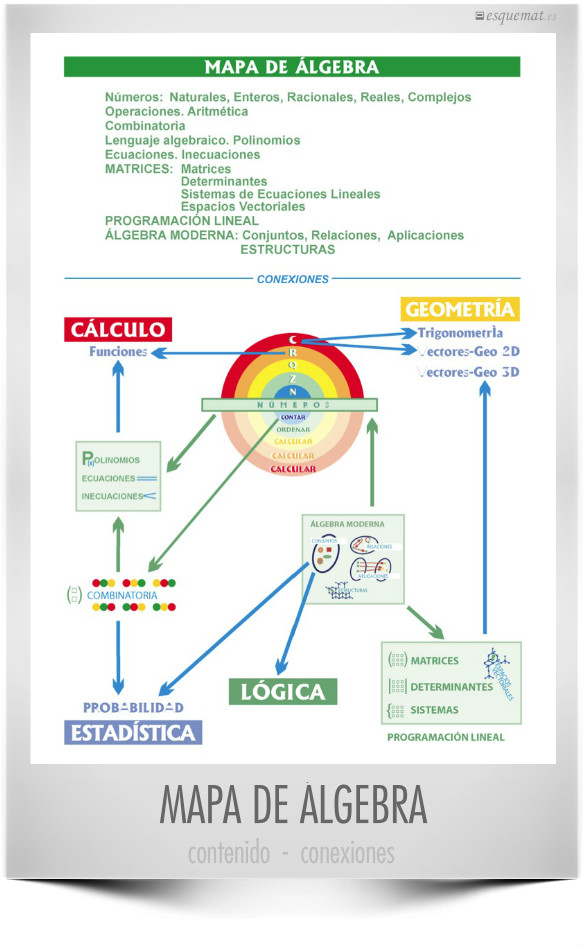
Los contenidos del Álgebra a nivel básico y sus conexiones con las otras ramas de las Matemáticas.
Guía: Clic en la imagen abre el esquema en pdf. Se puede imprimir y usar como mapa, coloreando las partes que se van recorriendo.
Guía prof: La inteligencia es en gran medida la capacidad de relacionar cosas. De ahí la importancia de ofrecer una visión de conjunto que ayude a construir el conocimiento.
Este esquema presenta los temas habituales de nivel secundario.
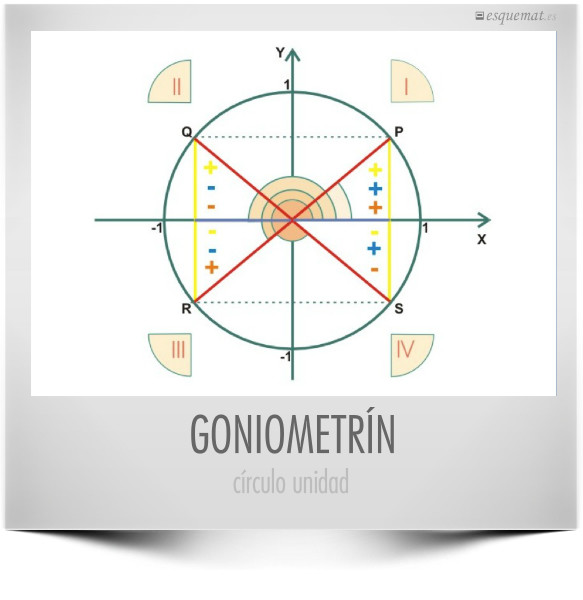
La circunferencia goniométrica permite situar en los ejes de coordenadas los ángulos y sus razones trigonométricas. Este dibujo sirve para reducir al 1º cuadrante los ángulos de los cuatro cuadrantes.
Guía:
Ayuda mucho tener siempre delante este dibujo cuando se trabaja con trigonometría.
Los cuadrantes se numeran con I, II, III y IV y en cada uno de ellos aparecen el segmento y el signo del seno y el coseno. También está el signo de la tangente, pero no su segmento, que estaría fuera de la circunferencia y que no hay que confundir con el radio que vale siempre 1.
Guía prof:
Clic en la imagen abre un pdf con goniometrines de 6×6 y 9×9 cm para imprimir en cartulina y repartir a los alumnos. El uso de términos desenfadados y poco formales quita aspereza a las Mats y llamarle goniometrín triunfa siempre entre los jóvenes.
Resulta más útil e instructivo relacionar las razones trigonométricas de los distintos cuadrantes por medio de la visión geométrica y la comprensión del significado que memorizando un montón de fórmulas del tipo sen (180+α)= −sen α

Los números complejos expresados en forma binómica y polar con su nomenclatura, operaciones en las dos formas y fórmulas de paso de una a otra.
Guía: Los nombres, símbolos y definiciones están en verde. Las fórmulas en rojo.
Clic en la imagen abre un pdf con la chuleta completa.
Guía prof: Puede completarse con la fórmula de Moivre y otras.
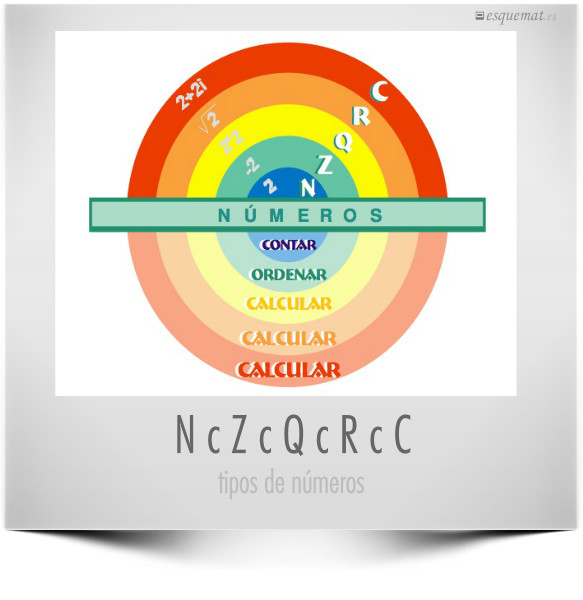
Los números naturales, enteros, racionales, reales y complejos, cada conjunto amplía el anterior.
Guía: Conviene saber en cada momento con qué números se está trabajando. Este esquema es un diagrama de Venn que representa que unos conjuntos están dentro de otros y puede ser un bonito cartel o pegatina para alegrar el estudio de los números.
Clic en la imagen abre un pdf con este esquema, los nombres y símbolos de cada conjunto y las letras con que habitualmente se indican sus elementos.
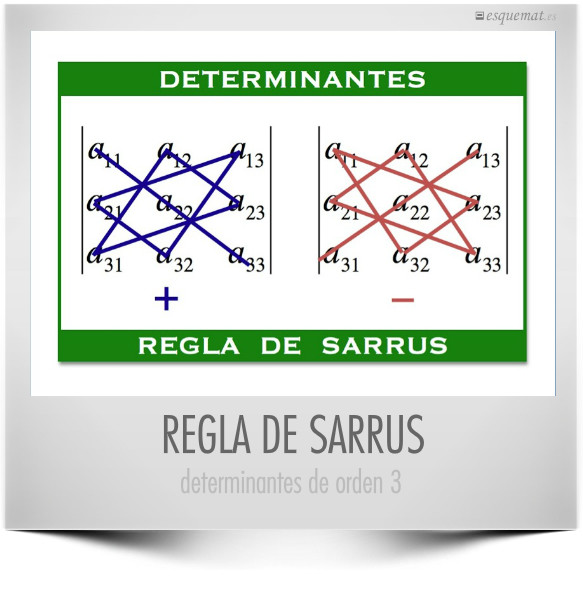
La regla de Sarrus para calcular el valor de un determinante de orden 3.
Guía: Un determinante es un número y para obtenerlo se suman los productos de los trios de números unidos por líneas azules y se restan los productos de los unidos por las rojas.
Clic en la imagen abre un pdf con este esquema y el desarrollo algebraico del determinante.
Además de escribir docenas de libros el gran Leonard Euler destacó por su agudeza y acierto en inventar nomenclaturas y notaciones. A él se deben la forma de nombrar los triángulos, la i de los números complejos, la Σ del sumatorio, la f(x) de las funciones, la notación de las funciones trigonométricas, la e como base logarítmica y exponencial, llamada hoy número de Euler, y la popularización del nombre y símbolo de π.
Su obra es inspiración y ejemplo para el inicio de este proyecto.