Imagen del método de Liu Hui para calcular la altura de una torre. Parece que se basa en proporciones sin llegar a la trigonometría con ángulos.
Una interesante visión histórica publicada en un libro del siglo XIII y divulgada por Maria João Lagarto autora de una inmensa recopilación de mates en su pinterest. Muito obrigado.
Archivo de la etiqueta: Trigonometría
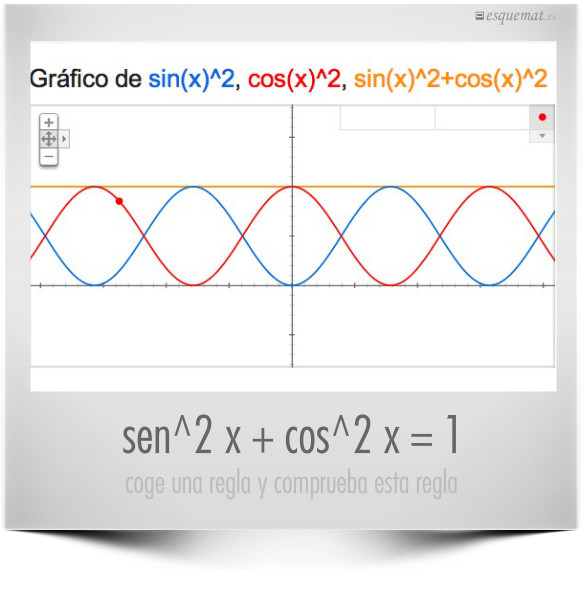
Sabido es que sen² x + cos² x = 1 para cualquier valor de x y aquí tenemos una interesante experiencia para una visión práctica de esta propiedad: Basta ir moviendo una regla a lo largo de las curvas y observar que la altura de la roja y la de la azul van sumando siempre lo mismo, la altura de la recta naranja, que es y = sen² x + cos² x = 1.
La precisión visual es escasa, pero la comprobación puede dejar un poso práctico del asunto.
Las gráficas están realizadas simplemente con google.
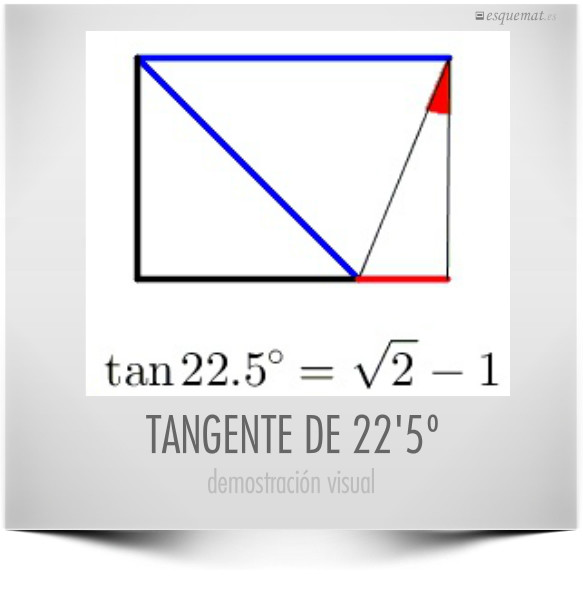
No sólo se pueden hacer buenos esquemas y diagramas para comprender las mates. También demostraciones visuales como esta que se puede proponer para que cada uno descubra su significado. Publicado en cut-the-knot.org

Cualquier método y soporte puede valer para un esquema, recordatorio o chuleta. Como éste que recuerda el teorema de Pitágoras y las definiciones de seno (sen ó sin), coseno y tangente (tag ó tan) de un ángulo en un triángulo rectángulo. A más de uña le encantará.
Clic en la imagen amplia la foto en sugarnails.
Entrada para la Edición 4.12310 del Carnaval de Matemáticas en el blog de @_mirandamolina_.
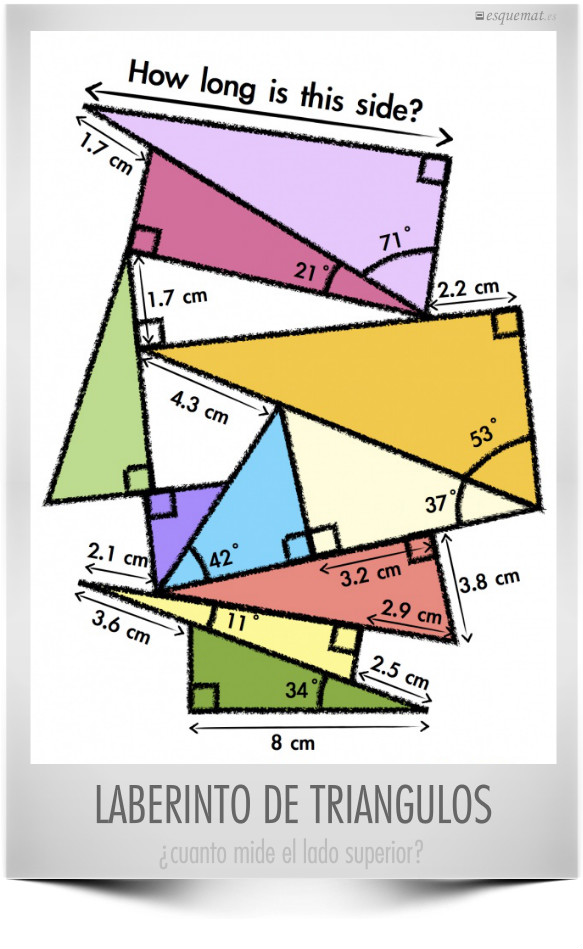
Partiendo de la base de 8 cm y con los datos de ángulos y segmentos que ofrece el dibujo hay que ir ascendiendo poco a poco hasta obtener la medida del lado superior, usando la trigonometría basica y el teorema de Pitágoras. Una idea interesante y efectiva que he utilizado desde hace años en mis clases, aunque no con un diseño gráfico tan logrado como este de greatmathsteachingideas.
Entrada para la Edición 4.1231 del Carnaval de Matemáticas en el blog i-matemáticas.com de JGM.
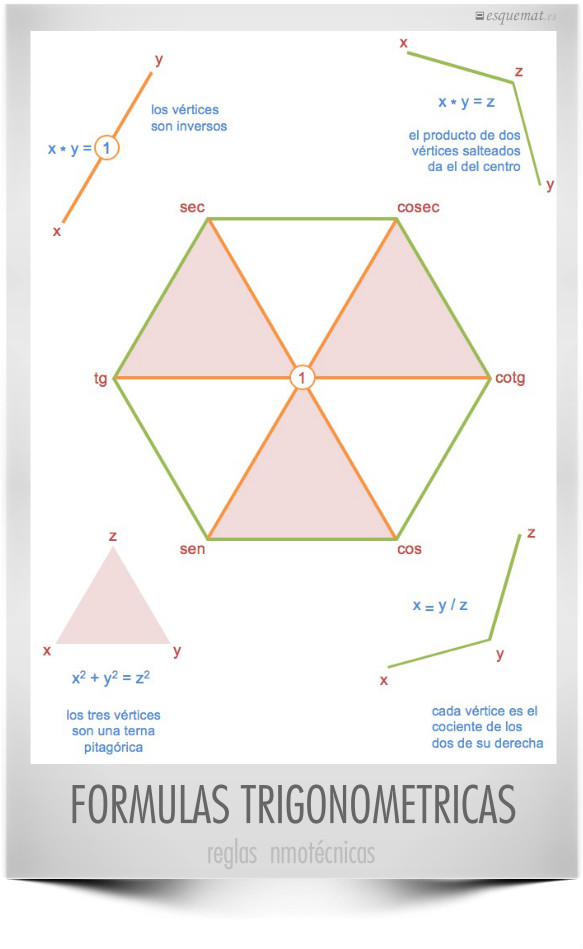
Las funciones circulares permiten obtener resultados de distintas maneras. Dándoles vueltas se vuelve a lo mismo. Este ingenioso hexágono permite recordar las fórmulas y relaciones básicas entre el seno, coseno, tangente, cotangente, secante y cosecante de un ángulo.
Muy ingenioso y creativo, perfecto para intrigar, investigar y jugar con los alumnos, la idea está tomada de Calvin en el blog.brilliant.org. Thanks!
Clic en la imagen abre un pdf ampliado a A4 con el esquema.
Esta entrada participa en la edición 4.123 del Carnaval de Matemáticas en el blog Eulerianos.
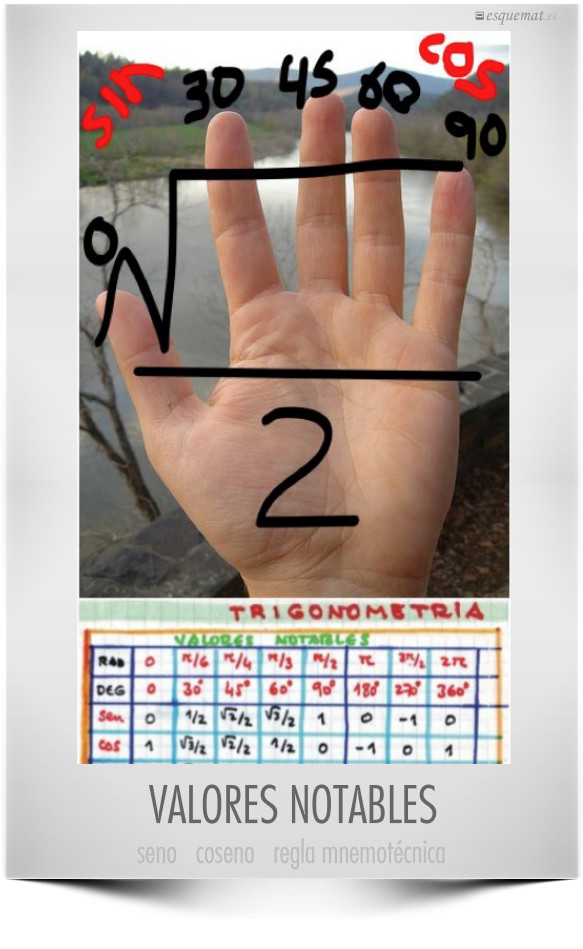
Hay una clásica regla para recordar los valores exactos del seno y coseno de 0°, 30°, 45°, 60° y 90° que consiste en escribir 0, 1, 2, 3, 4 y hacerle a cada número raíz y dividido por 2.
Ahora @k8nowak lo hace más fácil de recordar ilustrando esta regla con una fotografía en su blog function-of-time.blogspot.com.es.
Clic en la imagen abre un pdf en A4 con la foto y los valores en el esquemat trigonometría básica.

Formulario para resolver cualquier triángulo: Dados 3 datos (lados o ángulos) se deben hallar los otros 3 datos y el área. Cada fila es uno de los casos posibles y en ella se presentan las fórmulas correspondientes, que son los teoremas del seno y del coseno
Material: Clic en la imagen abre un pdf en A4 con el formulario y plantillas con datos de ejemplo y vacías, para proponer y resolver ejercicios o exámenes.
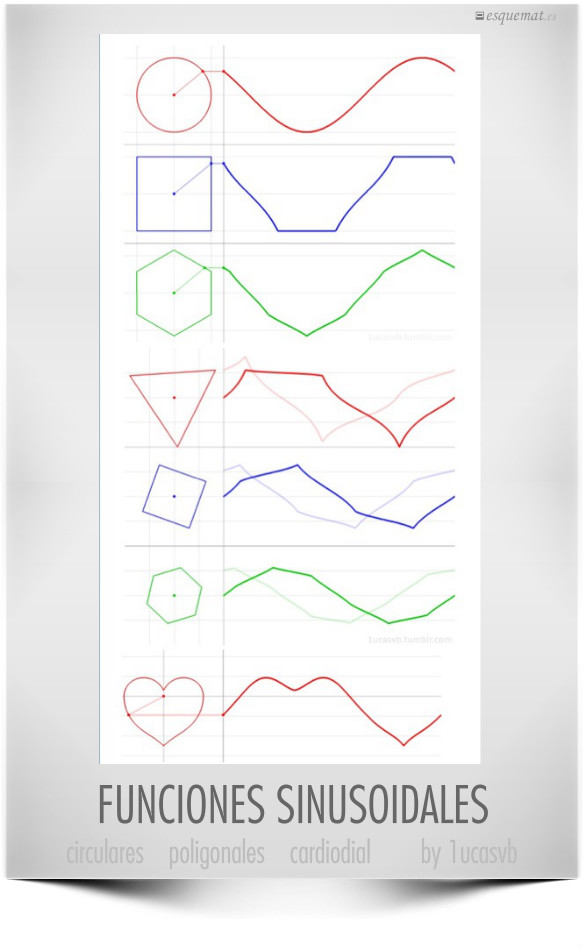
Infografía que captura las visualizaciones animadas de @LucasVB sobre las variantes de la idea de la función seno realizada sobre polígonos, sobre polígonos que giran y hasta sobre una cardioide.
Un trabajo extraordinario, con perfecta limpieza y sencillez de diseño que se inscribe en la más moderna tendencia de visualizamats.
Clic en la imagen abre un pdf con la infografía completa y la referencia a la web experimental de LucasVB, que es donde pueden verse las animaciones de cada caso.
Esta entrada participa en la Edición 4.1 del Carnaval de Matemáticas cuyo anfitrión es Tito Eliatron Dixit.

Formulario para resolver un triángulo rectángulo: Dados 3 datos (uno de ellos el ángulo recto A=90º) se deben hallar los otros 3 datos y el área. Cada fila es uno de los casos posibles y en ella se presentan las fórmulas correspondientes, que son las definiciones de seno, coseno y tangente y el teorema de Pitágoras.
El problema es sencillo con estas fórmulas y un simple dibujo del triángulo, por lo que lo más interesante para practicar y aprender es completar uno mismo este cuadro a partir de una plantilla vacía.
Material: Clic en la imagen abre un pdf en A4 con el formulario y dos plantillas en b/n, una con datos de ejemplo y otra vacía, para proponer y resolver ejercicios o exámenes.
Esta entrada participa en la edición 3.1415926535 del Carnaval de Matemáticas cuyo blog anfitrión es La Aventura de la Ciencia.