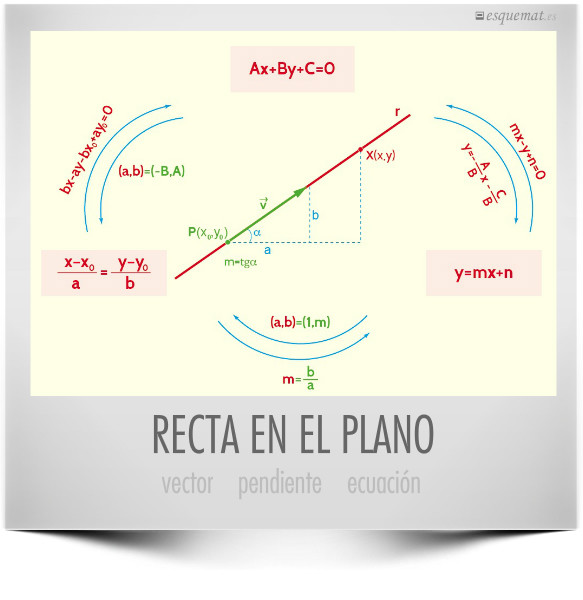
Esquema rápido que relaciona las formas principales de la ecuación de una recta en el plano y el modo de pasar de una a otra a partir de las relaciones entre coeficientes, vector y pendiente.
Es muy útil para comprender la ecuación de la recta y muy cómodo para usar como chuleta.
Click en la imagen abre este esquema en pdf completado con nomenclatura en español e inglés.
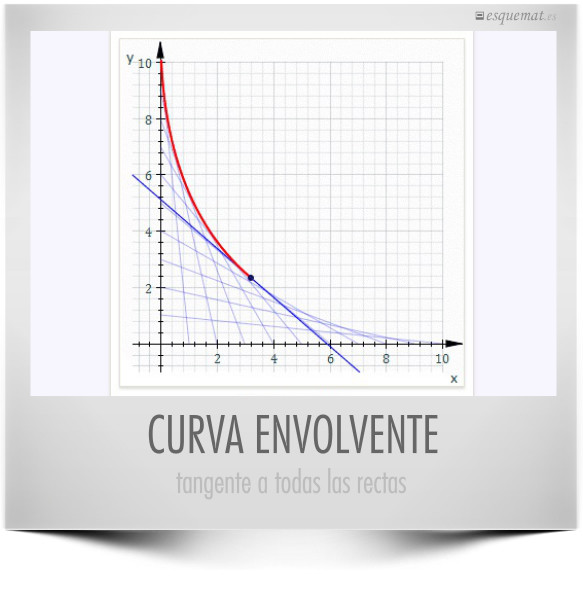
Se pueden dibujar curvas solo con rectas, obteniendo hermosas imágenes. Se trata de la envolvente, una curva tangente a una familia de rectas o de curvas, como vemos en el ejemplo publicado en el blog combinatórica:
¿Se puede expresar una realidad por medio de ecuaciones? Se puede. Y se hace en planos, proyectos y videojuegos. En esta foto se expresan en lenguaje de funciones líneas horizontales, del tipo y = b, verticales, x = a, oblícua, y = −x, en escalera, y = −[x], parte entera de x, todas ellas con ecuaciones, así como áreas rectangulares con inecuaciones, abarcando todos los puntos entre dos valores para la abscisa x y otros dos para la ordenada y.
Foto de fondo Armando Cuéllar.
Plantilla para plantear y resolver un multiejercicio sobre rectas en el espacio: Dados un punto y otro dato (punto, vector) o una ecuación, se debe rellenar la tabla obteniendo en cada caso todo lo demás.
Clic en la imagen abre un pdf con la tabla en A4, con un caso particular y una segunda tabla vacía para personalizar. Para editar completamente se puede descargar la tabla en formato .doc.
Plantilla para plantear y resolver un multiejercicio sobre rectas en el plano: Dados un punto y otro dato (punto, vector, pendiente, ángulo) o una ecuación, se debe rellenar la tabla obteniendo en cada caso todo lo demás.
Puede utilizarse el formulario recta en el plano.
Clic en la imagen abre un pdf con la tabla en A4, con un caso particular y una segunda tabla vacía para personalizar. Para editar completamente se puede descargar la tabla en formato .doc.
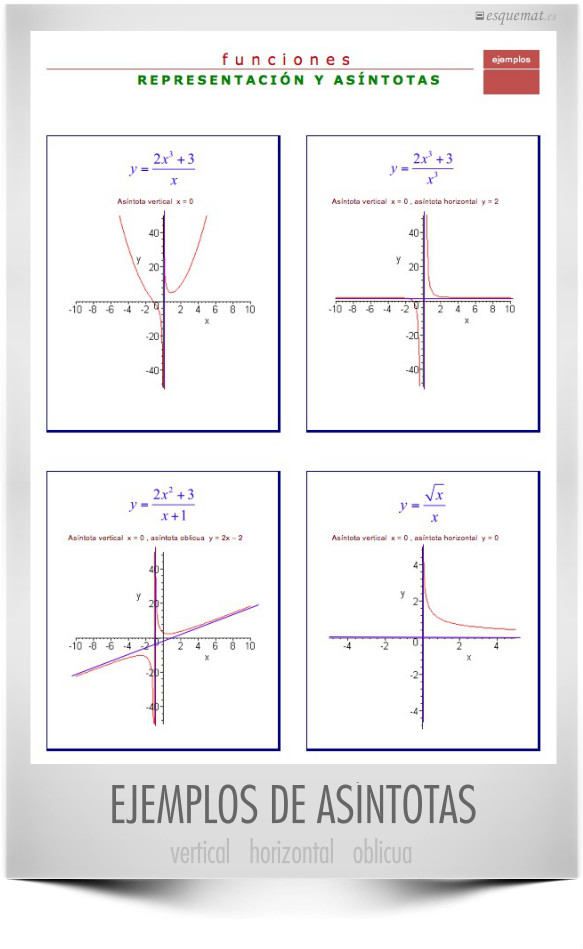
Algunos casos particulares de gráficas de funciones con sus asíntotas como ejemplo que complementa el formulario para el cálculo de asíntotas.
Clic en la imagen abre un pdf en A4 con los ejemplos para ver, descargar o imprimir.
Sencillo formulario para hallar las ecuaciones de las asíntotas a una curva, verticales (x=a), horizontales (y=b) y oblicuas (y=mx+n) mediante límites.
Clic en la imagen abre un pdf en 21×21 cm con el formulario para ver, descargar o imprimir.
El problema: Se trata de hallar la ecuación de una recta a partir de dos datos (punto-vector, punto-punto, punto-pendiente ó punto-ángulo con OX) o bien de pasar de un modo de ecuación de la recta a otro a partir de esos datos o de alguna de las ecuaciones de la recta.
La herramienta: Un formulario direccional diseñado para consultar fórmulas junto al proceso más simple de utilizarlas. Para cada caso posible los datos están en verde y las incógintas a obtener en rojo. La tabla presenta las fórmulas y las flechas el camino a seguir, a veces pasando de un caso de datos a otro y siguiendo por él.
La técnica: Uno de los datos será necesariamente un punto, llamado (x₀,y₀) en el formulario. Se elige en la tabla la fila que corresponda al otro dato y a partir de él se aplican las fórmulas siguiendo el camino marcado hasta llegar al modo de ecuación deseado.
Con este cuadro pueden obtenerse todas las formas de ecuación de la recta a partir de dos datos o una ecuación.
La experiencia: Con este sistema mis clases de geo analítica cambiaron. Los conceptos se aclaran y los resultados llegan rápidamente. Es muy apreciado por los alumnos porque ayuda a organizar las ideas y salir del lío de tantas fórmulas y conceptos nuevos. El cuadro se va desarrollando en clase, a medida que se avanza en el tema, y luego pueden plantearse ejercicios a tabla vacía, quitando las fórmulas y sustituyendo los datos genéricos por números. Y proponiendo como examen completar un cuadro similar con nuevos datos los resultados han sido espectaculares en alumnos de 15 y 16 años.
El análisis: Como en todos los métodos muy guiados o de plantilla esto puede ser como aprender a andar con takataka y conducir a obtener resultados por imitación sin entender casi nada. El peligro es cierto, si sólo se usan estos métodos, igual que si la enseñanza se limita a cálculos y operaciones, pero si se combinan con creatividad y dinamismo para despertar curiosidad e iniciativa, los esquemas y formularios direccionales se convierten en aliados que recuerdan caminos y ahorran tareas pesadas y rutinarias. La misma realización colectiva de este formulario, buscando reducir al máximo datos y expresiones es muy formativa pues la síntesis requiere gran comprensión. El desafío es hacer y enseñar a hacer herramientas que permitan algo tan matemático como lograr el máximo de posibilidades con el mínimo de recursos.
Material: Clic en la imagen abre un pdf en A4 con el formulario y dos plantillas vacías, en color y b/n, para proponer y resolver ejercicios o exámenes.
Esta entrada participa en la edición 3.1415926535 del Carnaval de Matemáticas cuyo blog anfitrión es La Aventura de la Ciencia.
Nomenclatura y formulario con los distintos modos de expresar la ecuación de una recta en el plano, a partir de dos puntos, punto y vector, punto y pendiente…
Guía: Como es habitual en esquemat, se presentan los datos en verde y las fórmulas en rojo.
Clic en la imagen abre un pdf con el formulario en A4 para descargar o imprimir.
Guía prof: Puede completarse el estudio de las rectas de manera práctica con el pendientímetro.
Con esta sencilla herramienta se puede medir la pendiente de una recta, en el papel o en la pizarra, o dibujar la recta a partir de su pendiente. Sirve para comprender mejor la geometría analítica plana y es útil también al estudiar las derivadas. Fué realizado en clase por Yasmina Perea, alumna de 1º de Bach.
Guía: Clic en la imagen abre un pdf con una plantilla para realizar un pendientímetro de 16 cm de diámetro.
