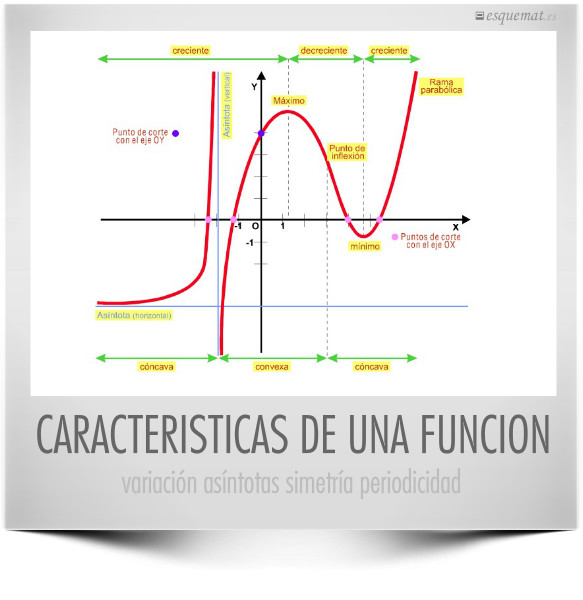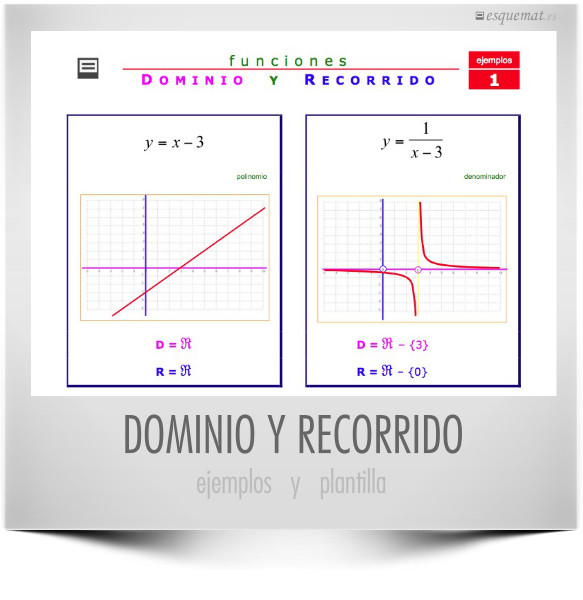
Ejemplos del dominio y recorrido de funciones polinómicas, racionales e irracionales a partir de la visión de sus gráficas.
GuÃa:
Clic en la imagen abre un pdf con 4 páginas de ejemplos y una plantilla para ver, descargar o imprimir.
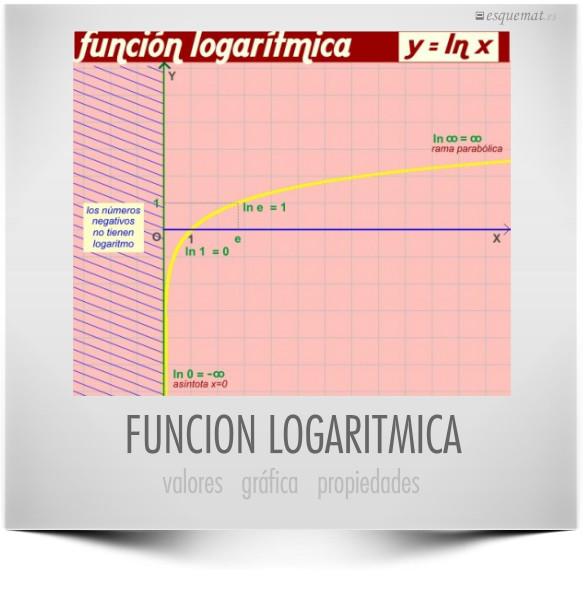
La función logarÃtmica con base e , su gráfica, dominio, recorrido y propiedades básicas.
GuÃa:
La gráfica ilustra que sólo los nº positivos tienen logaritmo y el comportamiento de la función en el cero y el infinito.
Clic en la imagen abre un pdf más amplio, donde además de la gráfica aparecen los valores y propiedades.
GuÃa prof:
Igual que en la vida aprendemos y recordamos más por una imagen que por largas descripciones, conocer la cara de las funciones y saber verlas es un recurso pedagógico extraordinario.
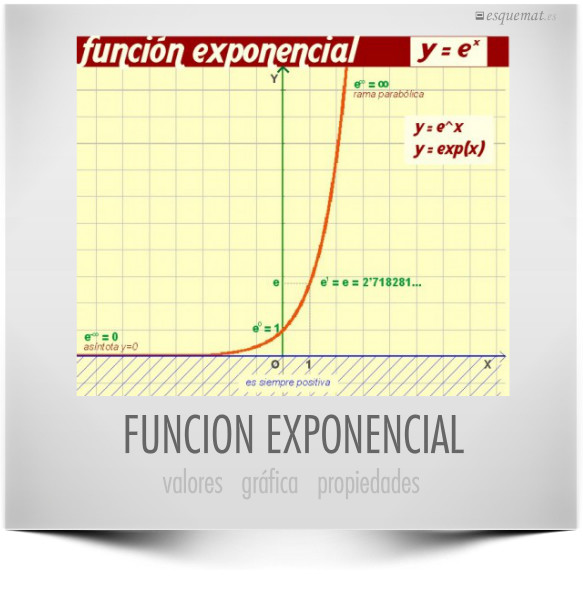
La función exponencial con el valor del número e , su gráfica, dominio, recorrido y propiedades básicas.
GuÃa:
La gráfica ilustra el comportamiento en el infinito, diferente por ambos lados.
Clic en la imagen abre un pdf más amplio, donde además de la gráfica aparecen los valores y propiedades.
GuÃa prof:
Tener siempre presente la gráfica con los valores principales al trabajar con esta función permite conocerla y trabajar mejor con ella, sobre todo en caso de lÃmites.
El word y otros procesadores de textos tienen una opción para realizar esquemas por niveles, como éste de funciones que presenta las definiciones a conocer y las propiedades a demostrar.
GuÃa:
Clic en la imagen abre el esquema completo en pdf para ver, descargar o imprimir.
GuÃa prof:
Para poder editar el esquema y adaptarlo al gusto de cada uno puede descargarse en doc en este enlace esquema de funciones
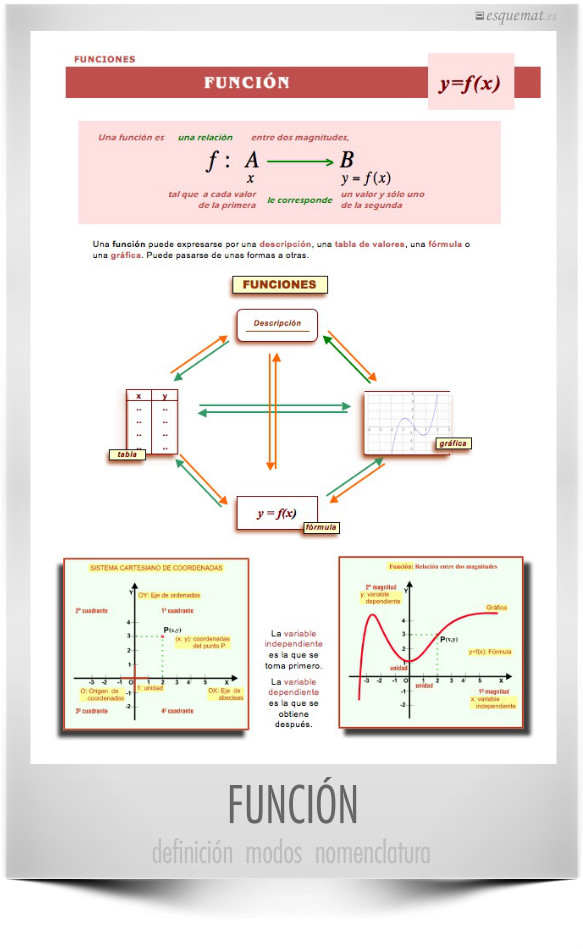
El concepto de función, base de todo el Cálculo Infinitesimal, con su definición, modos de expresión y nomenclatura.
GuÃa:
El concepto de función es sencillo cuando se conoce a fondo, pero ha costado muchos siglos llegar a él y perfeccionarlo. Al principio se hace abstracto por lo que es muy útil consultar un esquema claro e incluso aprender la definición, cuyo contenido va tomando luego sentido.
GuÃa prof:
Sólo el uso continuado de funciones en situaciones reales y problemas concretos va destilando el concepto de función, pero este esquema ha demostrado ser un buen apoyo. Cuando el nivel de abstracción es adecuado se puede definir en términos de conjuntos: “… una relación entre dos conjuntos tales que a cada elemento…”
