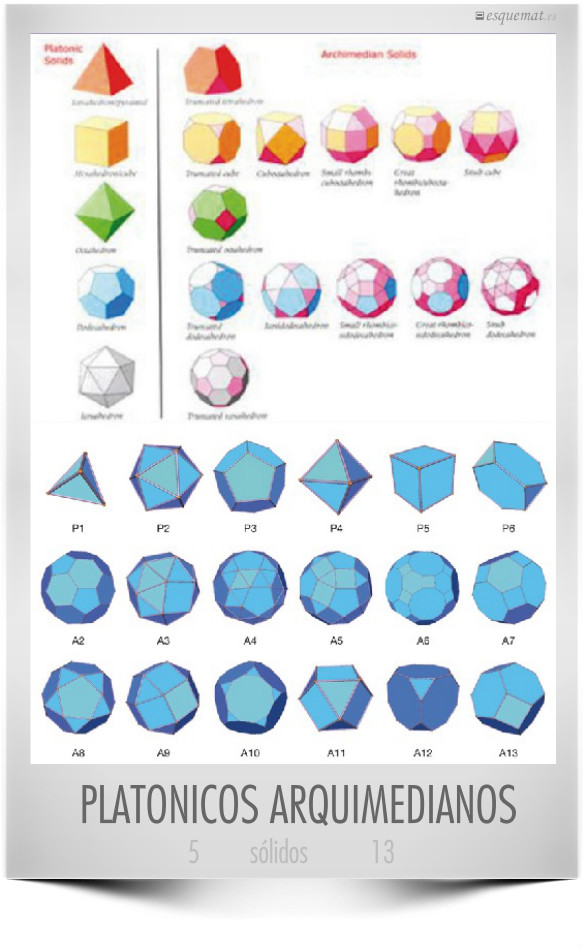
Dos visiones de los 5 sólidos platónicos, tetraedro, icosaedro, dodecaedro, octaedro y cubo, y los 13 arquimedianos, tetraedro truncado (A1), icosaedro truncado (A2), cubo chata (A3), desaire dodecaedro (A4), rombicosidodecaedro (A5), truncada icosidodecaedro (A6), truncada cuboctaedro (A7), icosidodecaedro (A8 ), rombicuboctaedro (A9), dodecaedro truncado (A10), cuboctaedro (A11), el cubo truncado (A12) y octaedro truncado (A13). Publicados en nature.
Archivo de la etiqueta: figuras
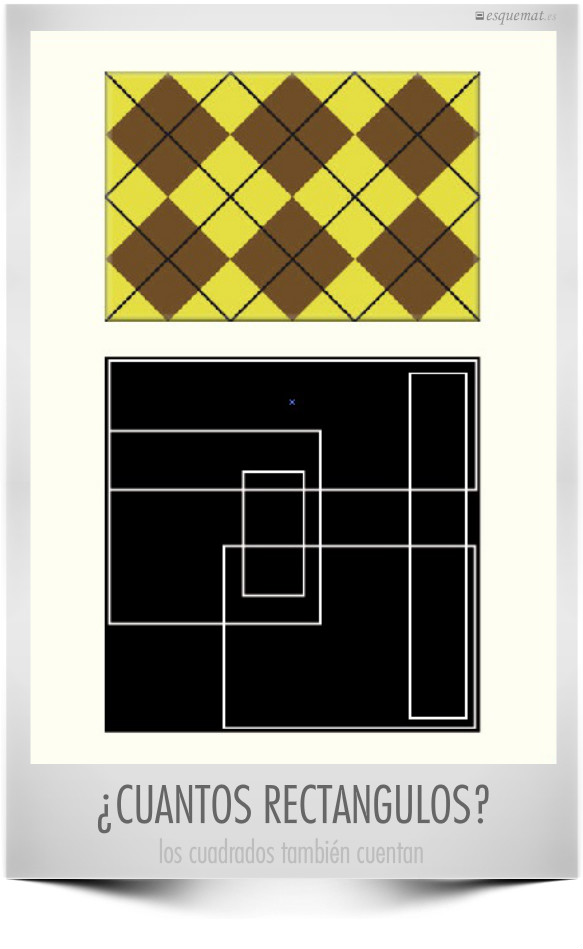
Un problema clásico, que puede plantearse con un fotomat o sobre dibujos geométricos.
Los originales son de transum.org, donde hay una versión pdf, y otras animadas e interactivas.
Clic en la imagen abre el esquemat en pdf.
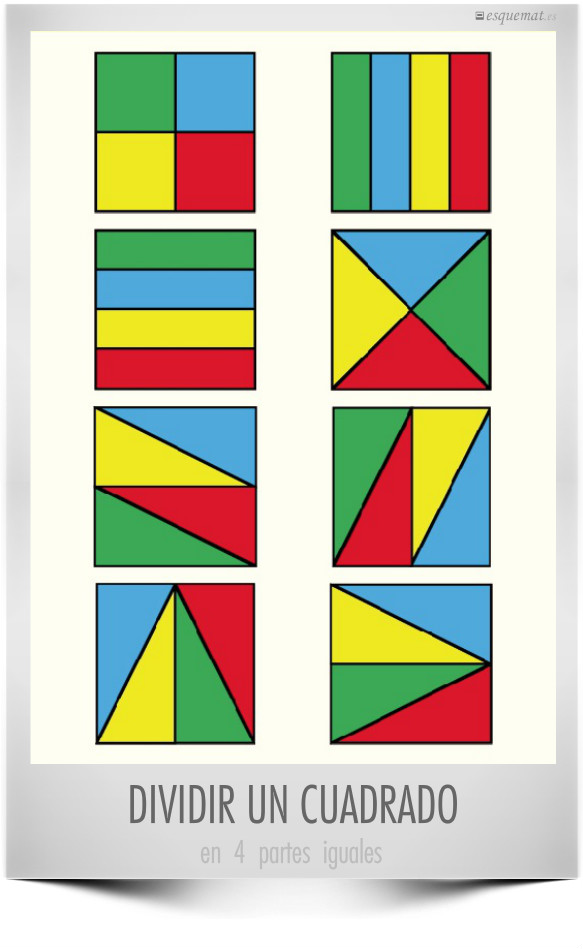
Un ejercicio sencillo para pensar y dejar investigar, dibujar cuadrados y dividirlos en 4 partes iguales. Hay muchas posibilidades y puede hacerse a mano o a máquina, digital, claro. Y se pueden probar otros caso, en 3 partes, en 6, con curvas…
Clic en la imagen abre un pdf con el esquema. Fuente Realm of Maths.
Esta entrada participa en la edición 4.1231056 del Carnaval de Matemáticas alojado en Scientia.

Porque jugar con las figuras y sus posibilidades y buscar formas hermosas también es una actividad creativa y matemática. Variantes de diseño sobre un hexágono, de la mano de Facu Ontivero.

Un juego increíblemente sencillo, divertido y estimulante para la mente. Se empieza pintando libremente cada hexágono de la fila superior de la plantilla de colores, azul, rojo o amarillo.
Y se sigue, fila a fila, con 2 reglas:
1- Si los dos hexágonos anteriores son del mismo color, el hexágono intermedio de la fila siguiente se pinta de ese color.
2-Si los dos hexágonos anteriores son de distinto color, el hexágono intermedio de la fila siguiente se pinta del tercer color.
Se producen multitud de situaciones distintas y se puede jugar a formar figuras, prever el color del vértice y a mil cosas que explican y muestran en pinkmathematics.
La idea original es de Steve Humble, publicada en el New York Times.
Y @Calaix2 recoge el juego en su Blog del Calix +ie en un detallado y bien ilustrado post y amplía el desafío con distintas opciones y materiales. Ánimo y ¡a jugar!
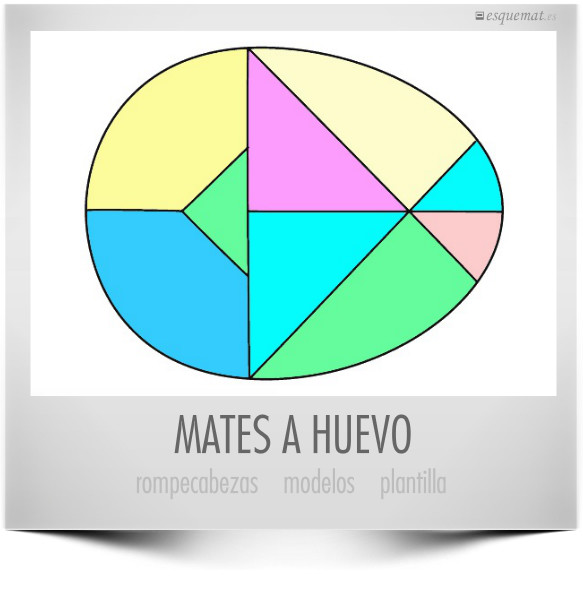
Ingredientes: Modelo ovoide con partición de colores y plantilla imprimible para recortar las piezas.
Receta: Imprimir la plantilla, colorear (opcional), a mano o digital, y recortar las piezas.
Modo de empleo: Repartir las piezas y tratar de formar, usándolas todas, las aves publicadas en nrich.maths y que se encuentran también en el doc BirdsToMake. Al terminar hay que formar de nuevo el huevo sin mirar el despiece.
Es una variante del tangram.

El gusto por la geometría entra por los ojos. Y por el trazado de figuras. Sirvan de inspiración los pósters geométricos de Amanda Rohlin.


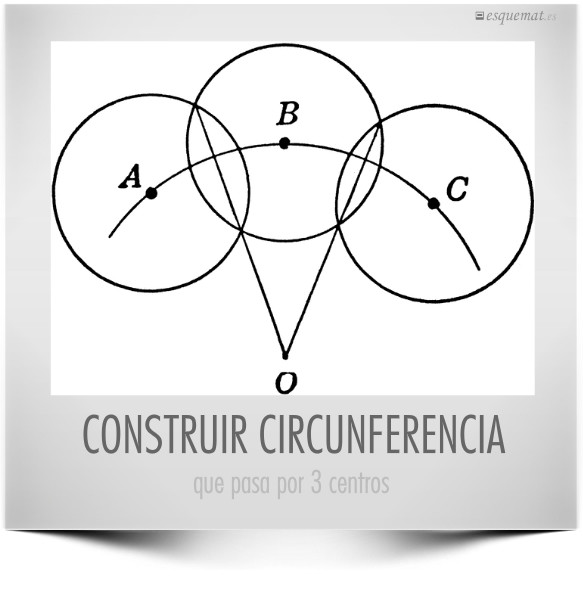
Construcción de la circunferencia que pasa por los centros de 3 circunferencias que se cortan dos a dos. Habría que recuperar en la enseñanza de las mates el desafío de las construcciones geométricas. Pueden verse muchas y buenas en el blog ClipArtETC, un recurso limpio y claro con muchas mates y otras materias.

Colección de bloques isométricos para crear mundos en miniatura en videojuegos. Moderna geométrica con infinitas posiblidades. Realizados por Hakán en monovektor.

Una sencilla chuleta para recordar y aprender los nombres de los polígonos en inglés. Publicado en twocandoit.


