Publicado el por
4

NUMEROS COMPLEJOS
Póster del conjunto de los números Complejos que destaca el símbolo C con el que se denota el conjunto, indica las operaciones posibles, muestra los ejes con los números reales como componentes y ejemplos de representación de complejos como vectores, con un guiño en los colores que indica que contiene a los naturales, los enteros, los racionales y los reales y expone de manera concisa su definición como un par ordenado de números reales.
Diseño original de @notemates para esquemat.es: Versión imagen sin marco. Versión pdf A4.
Entrada para la Edición 4.1231 del Carnaval de Matemáticas en el blog i-matemáticas.com de JGM.

Publicado el por
4

NUMEROS REALES
Póster del conjunto de los números Reales que destaca el símbolo R con el que se denota el conjunto, indica las operaciones posibles, muestra como ejemplo algunos números de distintos tipos, en particular π, e y Φ, con un guiño en los colores que indica que contiene a los naturales, los enteros y los racionales, y expone de manera concisa su definición axiomática y los nombres de otras formas de construcción de este conjunto.
Diseño original de @notemates para esquemat.es: Versión imagen sin marco. Versión pdf A4.
Entrada para la Edición 4.1231 del Carnaval de Matemáticas en el blog i-matemáticas.com de JGM.

Publicado el por
9

NUMEROS RACIONALES
Póster del conjunto de los números Racionales que destaca el símbolo Q con el que se denota el conjunto, indica las operaciones posibles, muestra como ejemplo algunos números de distintos tipos, decimales y fraccionarios, con un guiño en los colores que indica que contiene a los naturales y a los enteros, y expone de manera concisa su definición como conjunto cociente de una relación de equivalencia entre pares de números enteros, en el que el segundo término no es 0.
Diseño original de @notemates para esquemat.es: Versión imagen sin marco. Versión pdf A4.
Entrada para la Edición 4.1231 del Carnaval de Matemáticas en el blog i-matemáticas.com de JGM.

Publicado el por
12

NUMEROS ENTEROS
Póster del conjunto de los números Enteros que destaca el símbolo Z con el que se denota el conjunto, indica las operaciones posibles, muestra como ejemplo los primeros números positivos y negativos, con un guiño en los colores que indica que contiene a los naturales, y expone de manera concisa su definición como conjunto cociente de una relación de equivalencia entre pares de números naturales.
Diseño original de @notemates para esquemat.es. Versión imagen sin marco. Versión pdf A4.
Entrada para la Edición 4.1231 del Carnaval de Matemáticas en el blog i-matemáticas.com de JGM.

Publicado el por
14

NUMEROS NATURALES
Póster del conjunto de los números INaturales que destaca el símbolo IN con el que se denota el conjunto, indica las operaciones posibles, muestra como ejemplo los primeros números y expone de manera divulgativa, no rigurosa, los Axiomas de Peano con que se definen.
Diseño original de @notemates para esquemat.es: Versión imagen sin marco. Versión pdf A4.
Entrada para la Edición 4.1231 del Carnaval de Matemáticas en el blog i-matemáticas.com de JGM.

Publicado el por
Responder

SER O NO SER
To be or not to be. El problema es ser o su complementario, no ser, y la unión con el complementario es el todo, así que ser ∪ no ser = todo. Un divertido ejemplo de uso del lenguaje matemático para promocionar obras literarias.
El diseñador gráfico Nicholas Weltyk expresa en posters de 12″x18″ tres obras de Shakespeare
ilustrando con gráficos matemáticos citas  de Romeo y Julieta, Hamlet y El sueño de una noche de verano. Shakespeare in Math.

Publicado el por
Responder

CALENDARIO ISOMETRICO
Montar un calendario temático siempre es una buena idea didáctica. Como este de la imprenta Risograf ilustrado con utopías geométricas basadas en medios tonos y tintas fluorescentes en papel artesanal, obra de Jp Rey.

Publicado el por
Responder

GIROS DE LA LUNA
La luna gira alrededor de la tierra, la tierra gira en torno al sol, el sol se mueve… un espectáculo fascinanterecogido en un dibujo muy simple pero hermoso de Verónica basado en una antigua lámina italiana del siglo XIX.

Publicado el por
1

GEOMETRIA DE LOS ARCOS
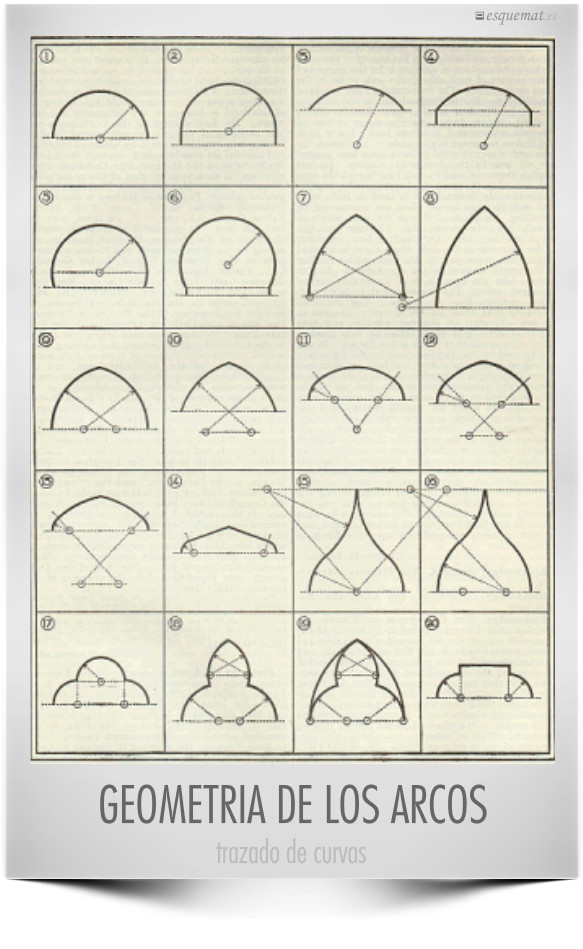
Una bonita panorámica de los distintos arcos desarrollados a lo largo de la historia de la arquitectura y su trazado geométrico. Para unir funciones, gráficas y curvas con geometría, estética y saber hacer.
Pueden verse detalles de su realización y fotografías en la cantería artifexbalear.org.

Publicado el por
Responder

ANATOMIA DE UNA MAGDALENA
Descomponer, factorizar ¿por qué sólo con números? Muchos procesos se pueden desmontar, analizando sus componentes, y aprender a razonar con ello, como en este póster con las partes de una magdalena, obra de Allen en Smart Batchs, donde nos regala también con un video del montaje del asunto.