
Una terna pitagórica está formada por 3 números enteros positivos a, b, c que pueden formar un triángulo rectángulo, es decir, que cumplen la fórmula del teorema de Pitágoras a² = b² + c². El gráfico muestra diversos casos ordenados según los estudios realizados en pythagoreantriples, blog especializado en el tema. Un buen tema para dejar que los alumnos investiguen y encuentren ternas y regularidades.

También usamos esquemas y diagramas sólo para profes. Como este que refleja qué multiplicaciones resultan fáciles o difíciles para los alumnos, según una investigación de The Guardian entre 232 estudiantes de primaria.

Otra forma de expresar la factorización de los enteros de 1 a 100 (de 1 a 70 en la imagen), ahora de manera divertida en un póster de Richard Evan Schwartz. Cada número primo es un personaje y los números compuestos son mezcla de sus factores personajes. Una original idea que puede servir para alegrar el aula, despertar la curiosidad y desafiar a los alumnos a realizar sus propias versiones.
Clic en la imagen abre el póster ampliado en una imagen pgn de 4482×4482 pixels.

Carteles con la descomposición en factores primos de los números del 1 al 100, donde cada primo está representado por un color y los compuestos se fraccionan en colores, según el número de factores. En la segunda versión se escriben también los factores primos correspondientes a cada color.
Clic en la imagen abre un pdf ampliado con los dos cuadros completos y una pequeña reseña.
Los diagramas están generados por software con un método de diferenciación de color, como explica su autor John Graham-Cumming, que se inspiró en un jersey tejido con esta idea.
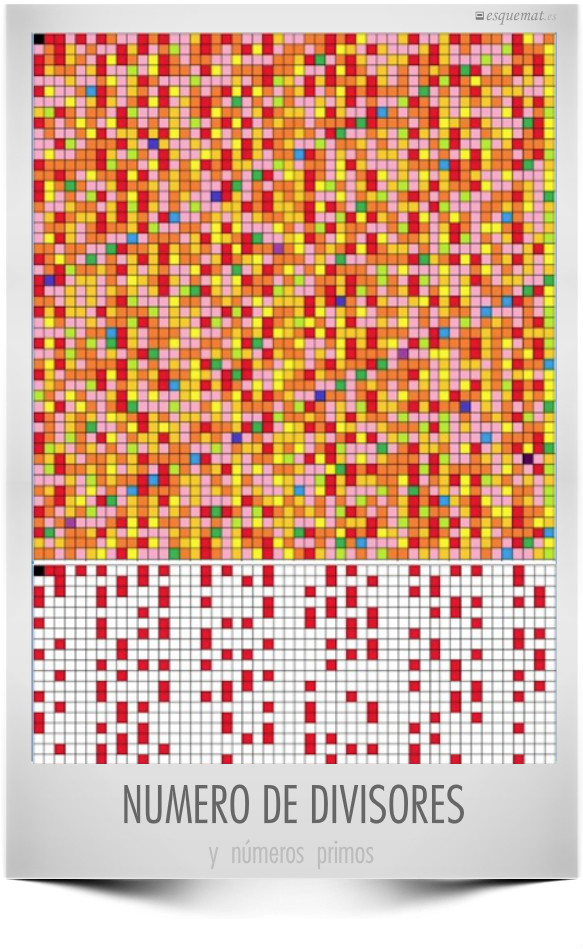
Cuadros coloreados que responden a las preguntas ¿Cuántos divisores tiene cada número? ¿Cuáles son primos? El primer cuadro, de 50×50 cuadritos, representa los números enteros del 1 al 2.500, cada fila corresponde a una cincuentena. El 1 es negro, los primos son rojos, los rosas son producto de dos primos, etc.
El segundo cuadro es el mismo salvo que se han quitado todos los colores menos el rojo: son los números primos.
No hay un patrón regular ni hay manera de predecir cómo será el siguiente. Pero el cuadro es interesante para practicar con divisores, comprenderlos y tratar de buscar regularidades. Y más aún para que los alumnos lo obtengan por sí mismos, partiendo de un papel cuadriculado y un puñado de rotuladores o con un procesador de textos u hoja de cálculo.
Clic en la imagen abre un pdf ampliado con los dos cuadros completos y una pequeña reseña.
Dibujos originales y comentarios en matheminutes.blogspot.fr.

Llenos de ideas, fórmulas y desarrollos, tremendos, eficaces y necesarios, olvidamos muchas veces incrustar la ciencia en sus raíces, buscar el de donde viene y dar a conocer a sus personajes. Podemos alegrar nuestras clases y apuntes con este póster psicodélico de Newton, de la serie Ciencia vs Delirium del diseñador australiano Simon Bent.

A partir de un triángulo equilátero y aprovechando cada vez un lado del polígono anterior podemos ir dibujando polígonos regulares. Un buen recurso para ver y dubujar imitando al diseñador Peter Hugo McClure.

Descubrimos un mundo infinito de poliedros, esta vez en base a cilindros del mismo diámetro y núcleos convexos. Hay muchos y de dos tipos, de caras estrelladas y de Johnson, en el poster ampliado de Fabio Zaplana.

Los deltaedros son poliedros cuyas caras son todas triángulos equiláteros iguales. Toman el nombre de la letra griega delta Δ, en forma de triángulo. Hay 8 clases de deltaedros convexos, dibujados sin colorear en la base del cartel de Fabio Zapata.

Para hacer buenos esquemas, materiales y presentaciones también son necesarios conocimientos básicos de fotografía. La regla de los tercios mejora la composición de las fotos y este original llavero de Marin Davide puede ayudar a ponerla en práctica.


