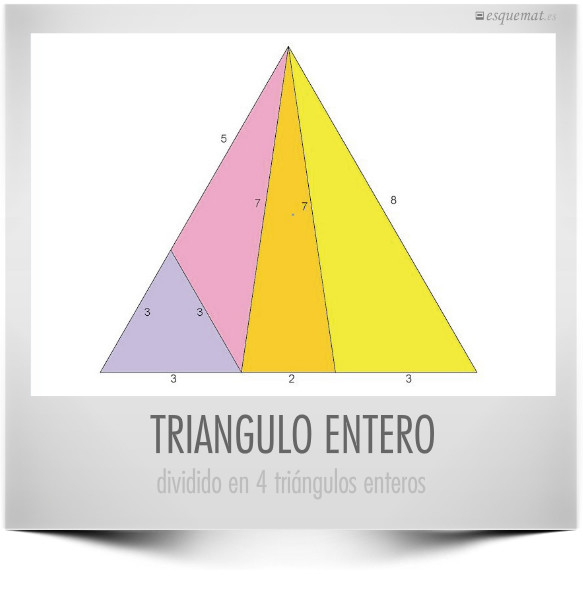
Un interesante concepto de dar formas a la FORMA en el logo del Concurso de Diseño Industrial para estudiantes rusos.
1
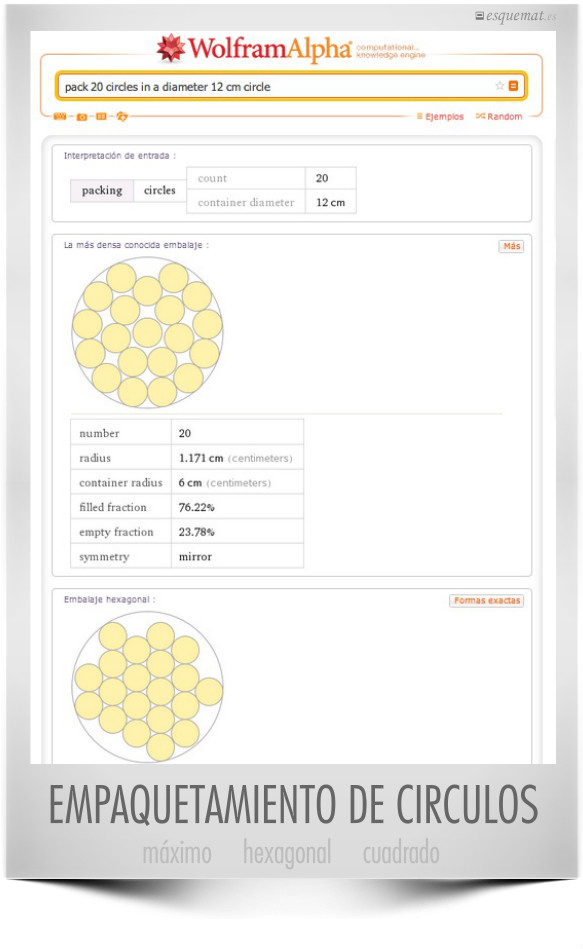
¿Cómo colocar n círculos en una circunferencia de diámetro m? Lo hace wolframalpha y lo recoge y explica Alex Zevallos en su práctico blog sobre el uso de esta magnífica herramienta.
Esta entrada participa en la edición 4.123105625 del Carnaval de Matemáticas en matesnoaburridas.
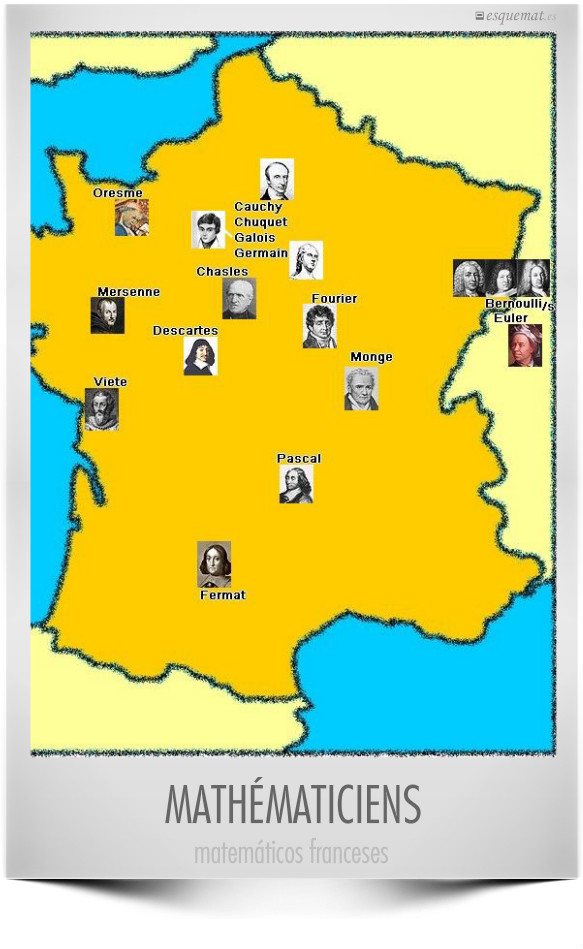
Algunos de los grandes matemáticos franceses clásicos, bien ubicados en el mapa por m@ths et tiques
Podemos jugar a … … de … …, como: primos de Mersenne, series de Fourier, fórmulas de Cardano-…, último … … de Fermat, coordenadas … … y mucho +
Nótese que no hay uno, sino varios Bernouilli’s.
Esta entrada participa en la edición 4.123105625 del Carnaval de Matemáticas en matesnoaburridas.
Con simples folios de colores y la técnica de Sonobe de Mitsunobu se pueden formar hermosas figuras 3D. Algunas de las más sencillas se explican paso a paso y con todo detalle en mathcraft, donde se encuentra además todo un mundo de Artesanía Matemática.
Algunos números enormes, bien explicados con detalle en 10 enormous numbers.
Clic en la imagen abre el esquemat en pdf.
Un documento histórico, de hace 400 años. La multiplicación no cambia, sólo el diseño y la forma de escribir han cambiado. Original de Galileo Galilei (1564-1642).
Enviado por @SilviaP313. Muchas gracias.
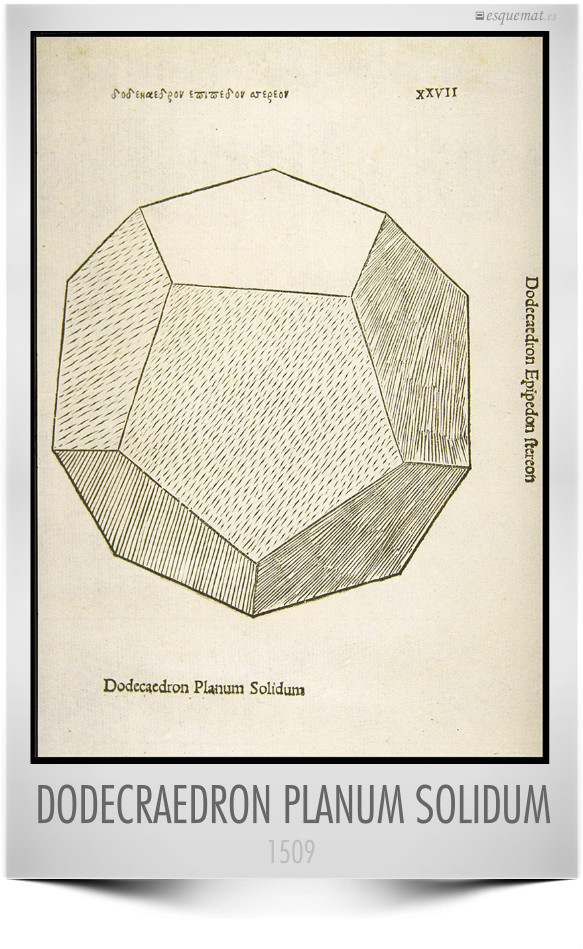
Dodecaedron Epipedon stereon, Dodecaedron Planum solidum de un libro de Pacioli, con una gran trabajo de diseño y sombras en el año 1509. Curiosamente tiene el mismo tema y el mismo fondo que el calendario de poliedros 2014 del esquemat de ayer. En todas las épocas ha habido un gran esfuerzo por representar las cosas más y mejor.
Cada año los calendarios son un buen soporte para expresar y recordar las mates. Este es una lámina de Julia Kostreva, a la venta en etsy.
Archie Archambault dice que un círculo es la forma más suave para el ojo, la más simple, la más hermosa y la más fácil de absorber la información.Y, así, hace mapas circulares de los barrios de las ciudades, ramas de gobierno y árboles genealógicos o un mapa del sistema solar con los planetas y todas sus lunas. No representa forma de las órbitas ni las distancias reales, pero sí expresa, como el famoso mapa topológico del metro de Londres, el espacio y las relaciones entre los objetos.
Hoy es día 11 del 12 del 13, 11/12/13, un día apropiado para ver los triángulos equiláteros e isósceles con lados enteros que busca y explica seekecho. Acceso con clic en la imagen.
