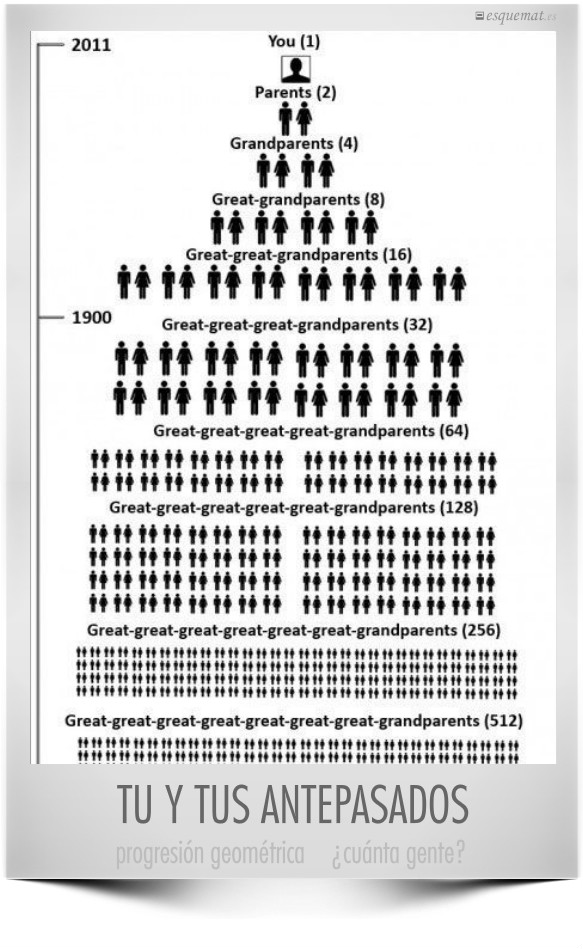
j Ahà donde te ves, tienes 2 padres, 4 abuelos, 8 bisabuelos y la cosa sube en progresión geométrica. Muy pronto se alcanzan cifras imposibles, si no fuera porque los antepasados se repiten, cada uno puede ser tatatarabuelo de muchos. Un interesante ejercicio de reflexión definico con humor como incestion.
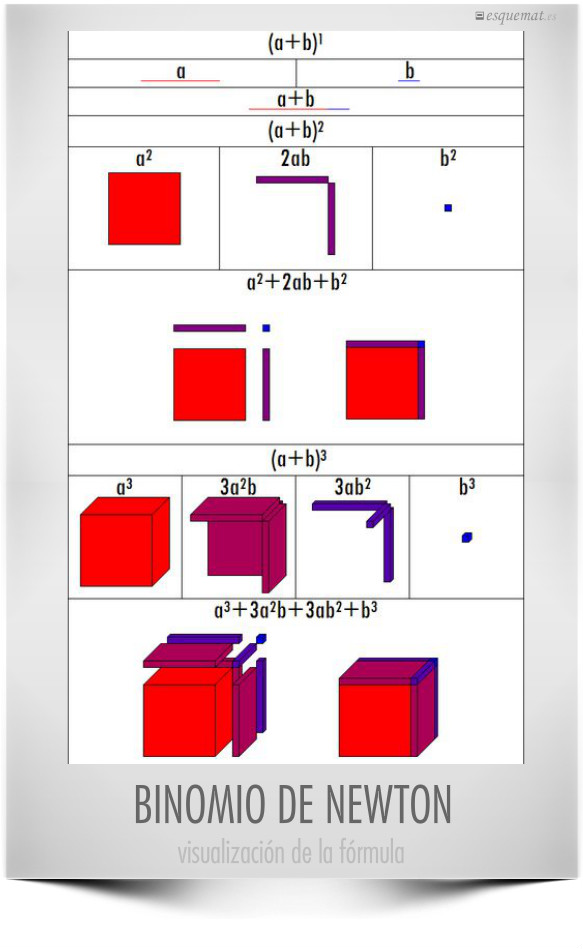
Ya es habitual representar gráficamente la fórmula del cuadrado de una suma (a+b)²=a²+2ab+b² y el autor de do-math da un paso más y nos dibuja la fórmula del binomio de Newton de grado 3. ¿Quien se atreve con la de 4º grado?
La espiral logarÃtmica gira sobre un eje y deja rastros desde 8 puntos prefijados, en un movimiento fascinante. Original en allofthemath.
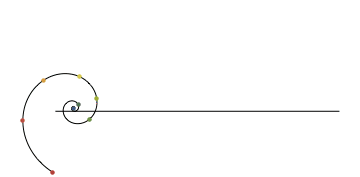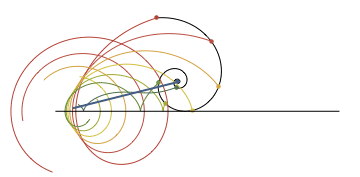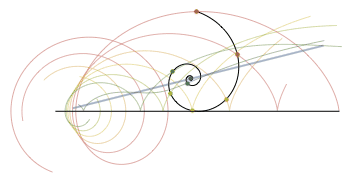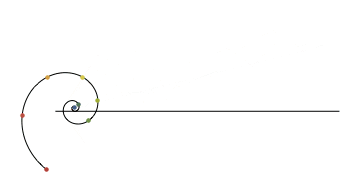
¿Qué polÃgonos se pueden dibujar tomando 1 vértice, 2, 3 … una sola vez? ¿Y tomándolos 2, 3, 4… veces? Una hermosa exploración de Zakir Gowani que llega hasta 6×6 al ampliar la imagen.
Un alegre póster para aprender a escribir las cifras contando y que puede servir para descubrir el trabajo de Nicole Holmes.
Otra experiencia matemática y artÃstica original del diseñador gráfico Marcos Gonyea que puede animar a realizar experimentos similares. Requiere contar de 1 a 100 formando imágenes,  figuras y simetrÃas en un trabajo sistemático, metódico y ordenado. Puras mates.
Estos pixeles participan en la edición 5.1 del Carnaval de Matemáticas en titoeliatrondixit.
Un mismo punto puede ser vértice de varios polÃgonos que lo rodean completamente. El blog de Don Steward nos muestra varios casos y nos invita a reflexionar sobre si otros son posibles no.
Esta entrada participa en la edición 5.1 del Carnaval de Matemáticas en titoeliatrondixit.
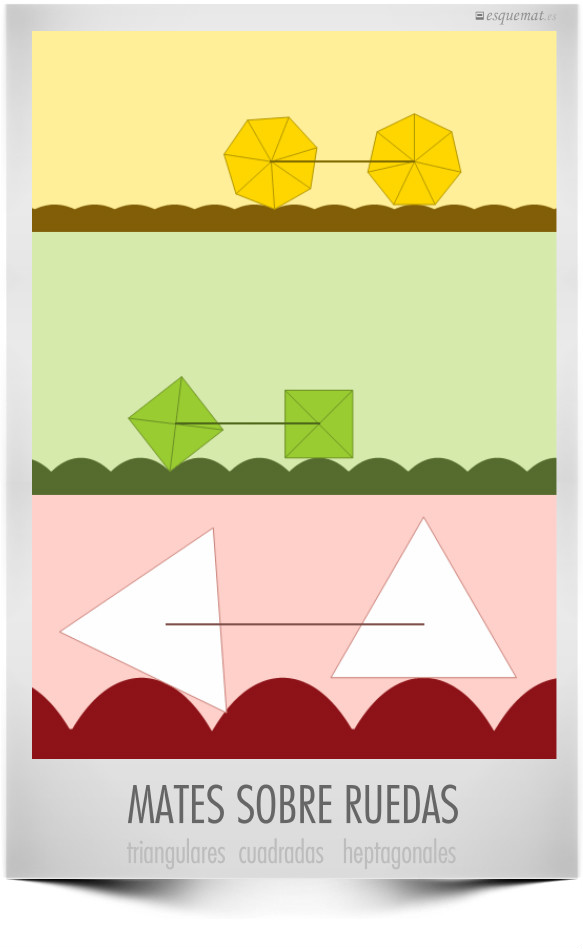
Las ruedas suelen redondas, lo que viene muy bien con un suelo plano. pero también hay quien se atreve a probar con ruedas cuadradas, adaptando el suelo con la curva catenaria conveniente. Un diseño animado por movies and math y hecho realidad en el MoMath, con un efecto mágico que no nos cansamos de ver:
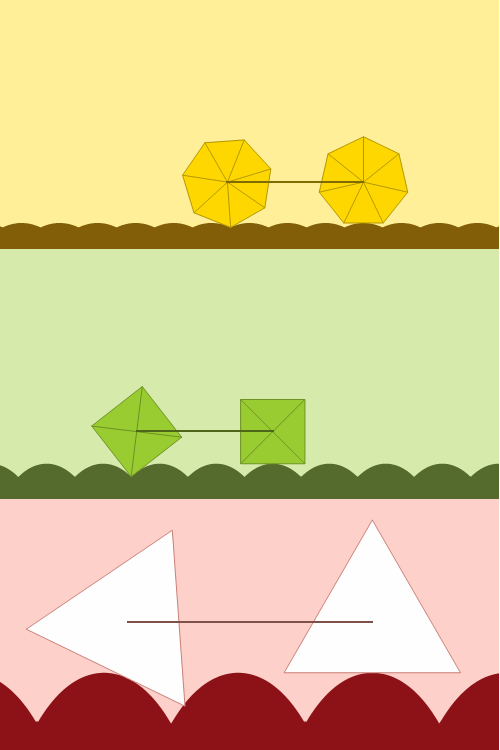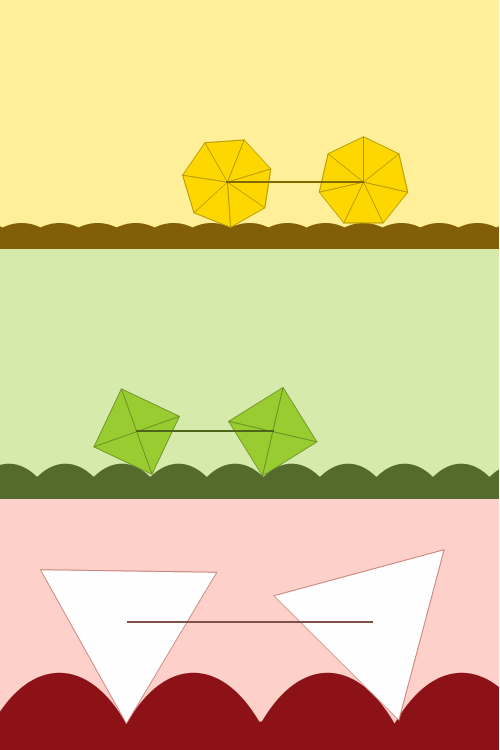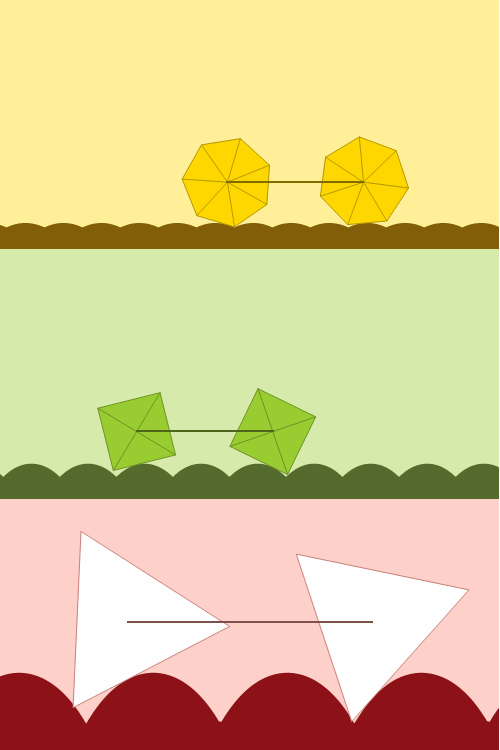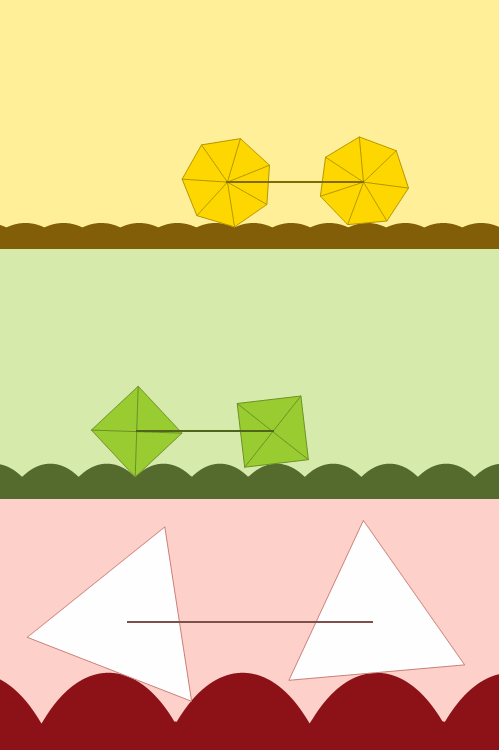Esta entrada participa en la edición 5.1 del Carnaval de Matemáticas alojado en titoeliatrondixit.
Usando en cada caso las mismas 7 piezas del tangram podemos formar estas 3 copas, pero una está completa y las otras  tienen huecos diferentes. La vista engaña, pero la geometrÃa no. ¿Qué es lo que ocurre?. Podemos resolverlo saboreando un tangranwich.
Sam Lloyd presentó esta paradoja en su libro Eighth Book of Tan de 1903. Imagen de wikipedia.
A BB CCC … y asà hasta ZZZZ… en una idea y diseño vistoso y bien trabajado de Mark Gonyea.
