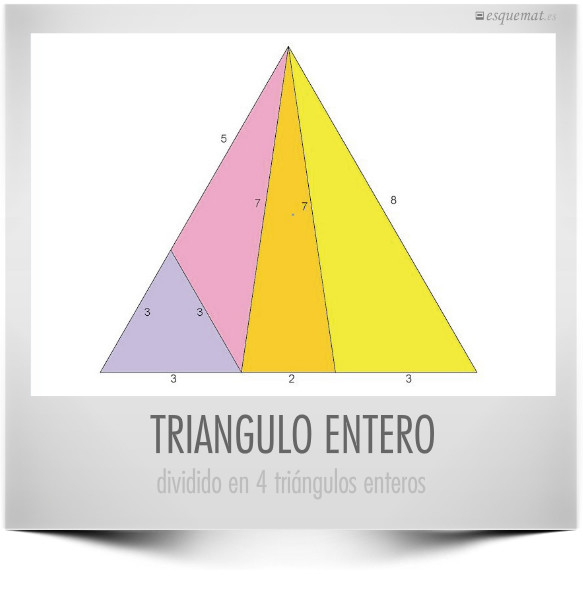
Hoy es día 11 del 12 del 13, 11/12/13, un día apropiado para ver los triángulos equiláteros e isósceles con lados enteros que busca y explica seekecho. Acceso con clic en la imagen.
Archivos Mensuales: diciembre 2013
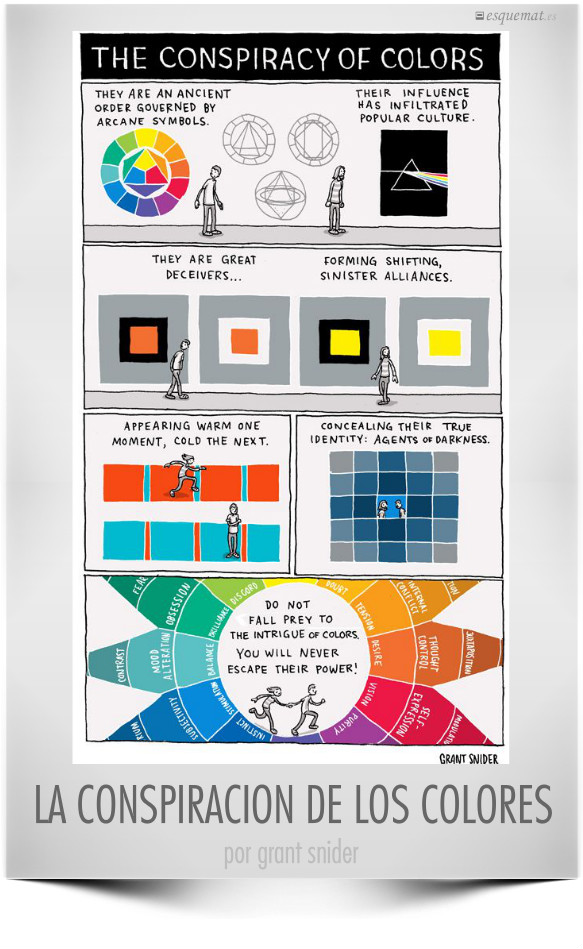
Si ayer traíamos la teoría formal del color hoy toca una visión desenfadada y audaz del gran Grant Snider.
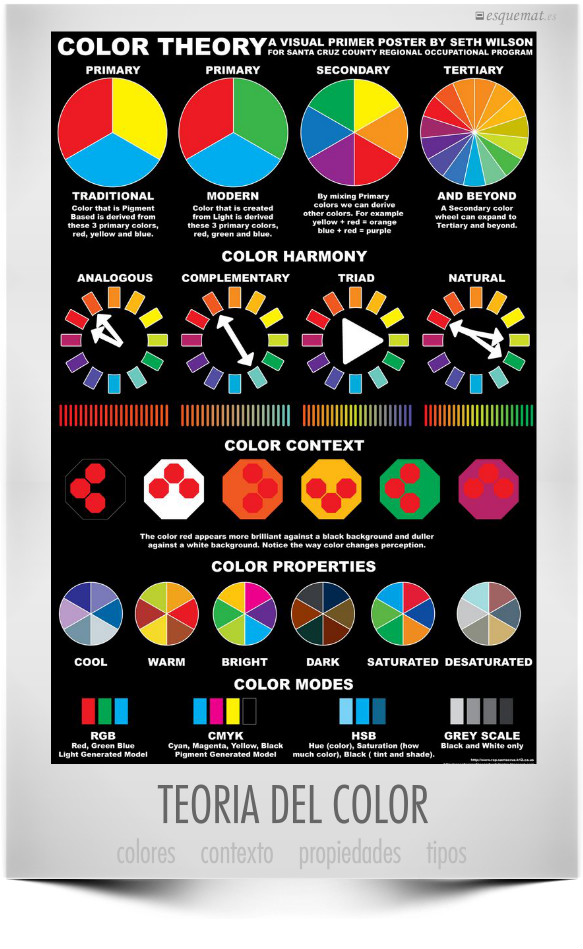
Para hacer buenos diseños hay que conocer las bases de la teoría del color. Este póster de Seth Wilson está realizado para sus alumnos y el autor anima expresamente a difundir, imprimir y utilizarlo en clase. Tiene diseños y pósters educativos de color y fuentes en su site en béhance.
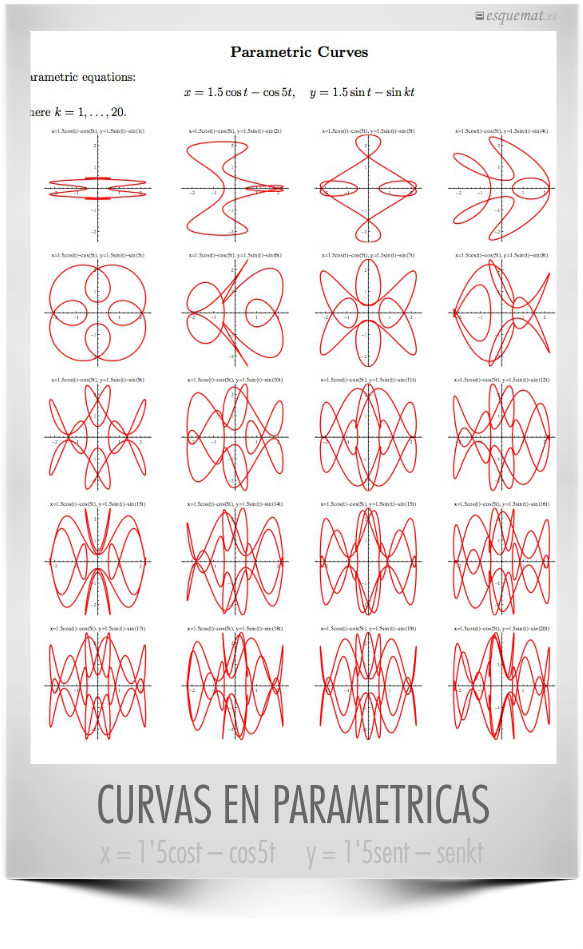
Las curvas en coordenadas paramétricas dan gráficas extraordinarias con expresiones sencillas gráficas, como las del esquema donde varía sólo k de 1 a 20 y otras muchas que se pueden ver bien ordenadas y explicadas en Parametric Curves de Kiryl Tsishchanka. Atiza diríamos al ver estas curvas desde fotomat.
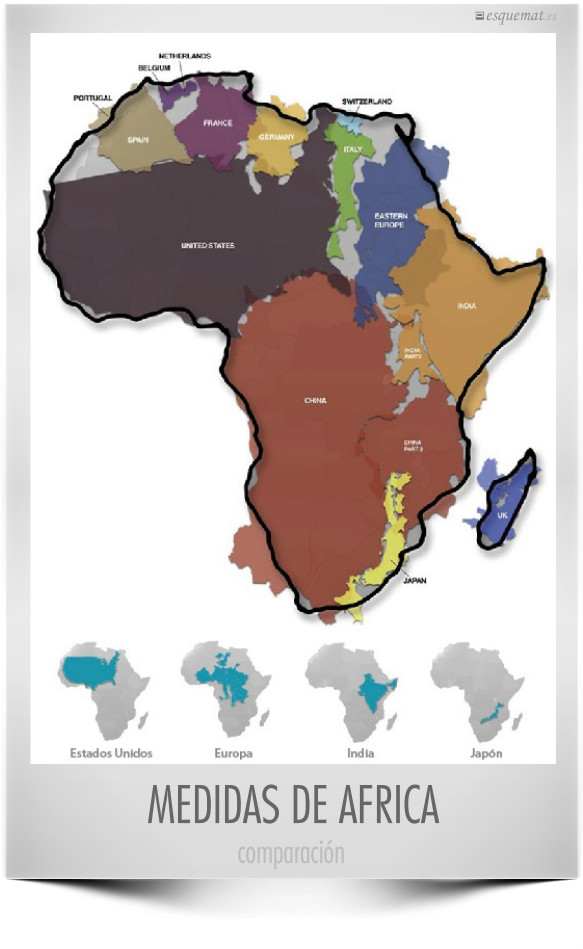
Una hermosa imagen comparativa de la superficie de África con la de distintos países del mundo. Muy bien documentado con el mapa y todos los datos.

La estructura hexagonal de los copos de nieve siempre ha fascinado a matemáticos y diseñadores. Aquí una lámina de 1863 que estudia el tema.
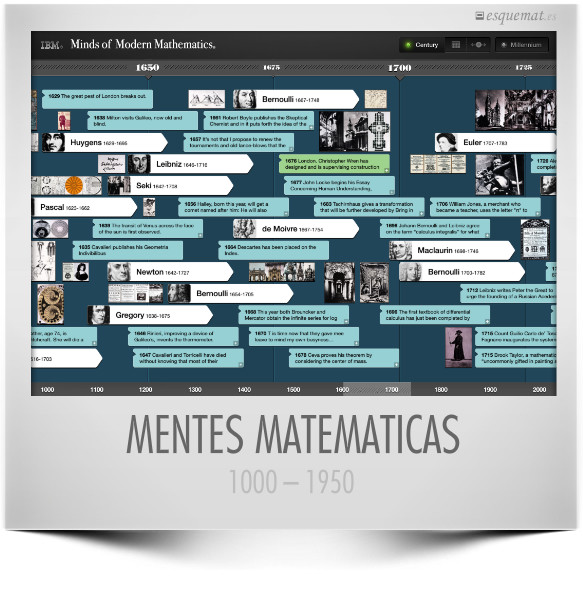
Mucho Más que un esquema, MMM, Minds of Modern Mathematics es una App de IBM que recorre fecha, imágenes, vida y obra, wikipedia y wolframalpha de 1000 años de Matemáticas. Y que IBM celebra recordando su Math expo de 1964. MMMM Mis Mates Me Molan Mucho.
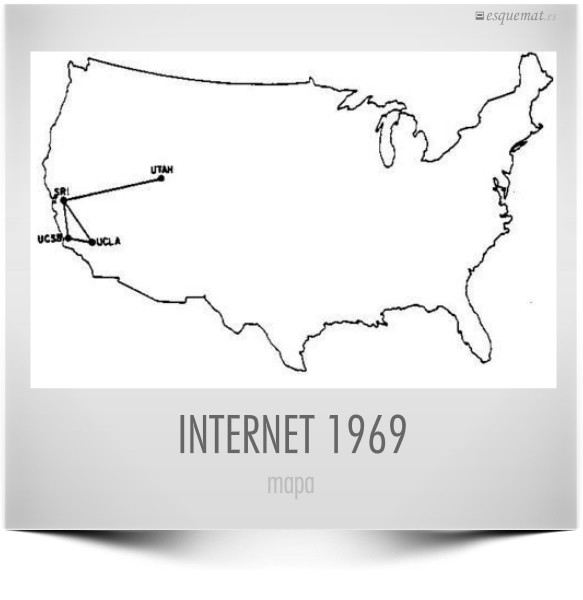
Cuando un mapa vale más que mil palabras. Por Erich Morisse.

Un diseño de Karel Martens que integra el símbolo 5 con su concepto ●●●●● en cinco piezas además color y formas que pueden utilizarse para diseñar otras cifras. En un día en que celebramos una suma que se multiplica por 5.
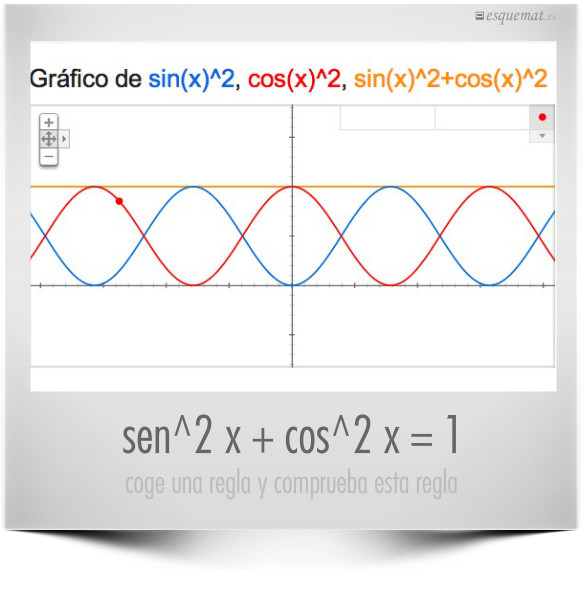
Sabido es que sen² x + cos² x = 1 para cualquier valor de x y aquí tenemos una interesante experiencia para una visión práctica de esta propiedad: Basta ir moviendo una regla a lo largo de las curvas y observar que la altura de la roja y la de la azul van sumando siempre lo mismo, la altura de la recta naranja, que es y = sen² x + cos² x = 1.
La precisión visual es escasa, pero la comprobación puede dejar un poso práctico del asunto.
Las gráficas están realizadas simplemente con google.