
Hay 512 maneras de colorear una cuadrícula de 3×3 con sólo dos colores. El problema equivale a colocar colores blanco y negro 9 veces en línea de todas las maneras posibles. Son las variaciones con repetición de 2 elementos tomados de 9 en 9: VR2,9 = 2⁹ = 512. Un interesante ejercicio para practicas con pautas y regularidades.
En la imagen aparecen sólo 368 de las 512 posibles. El original completo y ampliado puede verse en obsessedbythegrid.
Archivos Mensuales: julio 2013
❝En cuestiones de ciencia, la autoridad de mil no vale el humilde razonamiento de un solo individuo❞
Galileo Galilei
Porque no es lo mismo verdad que opinión. Visto en posterenvy.
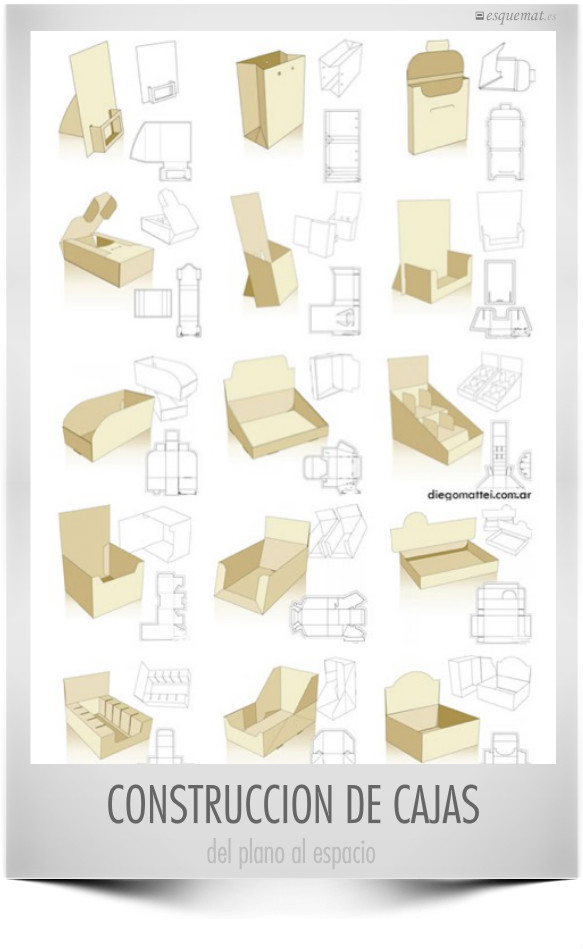
No son las figuras geométricas básicas, pero nada nos impide ampliar la visión, curiosidad y posibilidades de la geometría.
Clic en la imagen amplía el esquema con más casos en diegomattei.com.ar

Las reglas básicas de divisibilidad en una chuleta clara y colorista que sirve de paso para practicar vocabulario matemático en inglés. Póster a la venta en posterenvy.
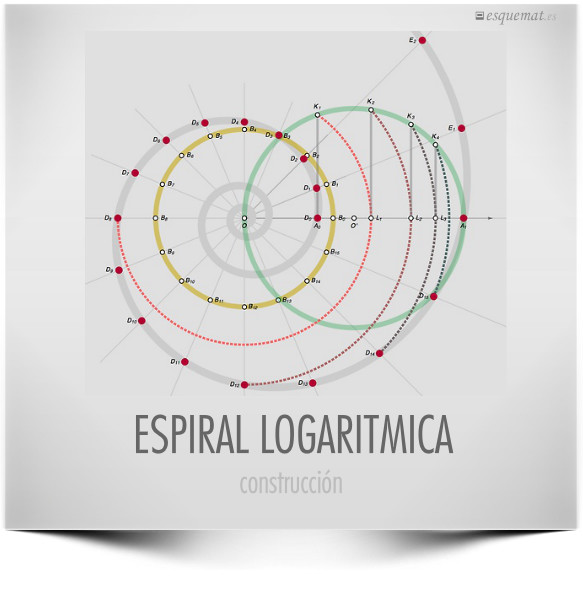
Una construcción de la espiral logarítmica, siguiendo M. Vygodsky, publicada en imathematicus.
Clic en la imagen la amplía a alta resolución.

Ingenioso kit que anima y enseña a descubrir y clasificar nubes y predecir el clima. Para imprimir, montar y usar, en venta en nature-watch.
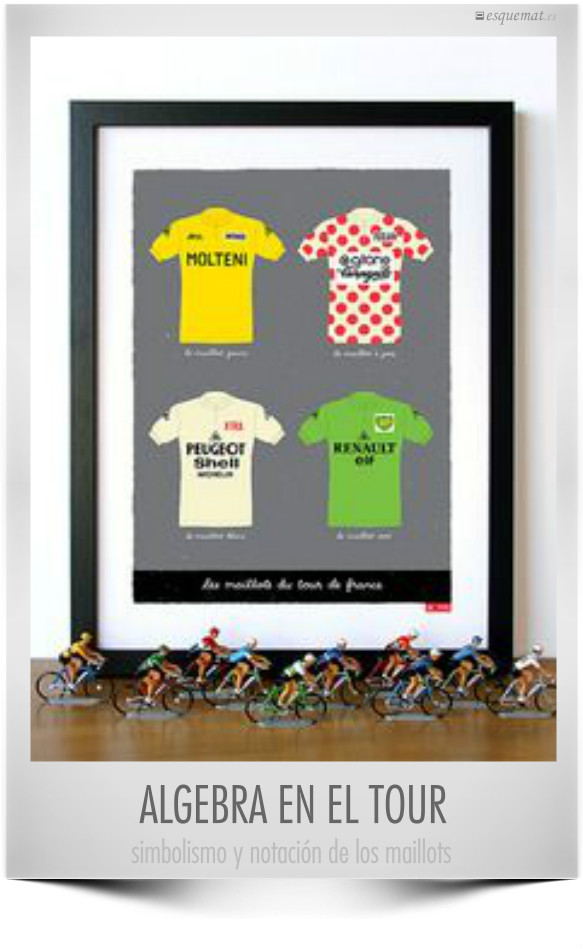
Amarillo para el 1º por tiempos, verde para el 1º por puntos (orden de llegada), moteado para puntos de montaña y blanco para el 1º joven por tiempos, códigos de color que facilitan la comprensión y el uso y equivalen a nombres de variables en el lenguaje algebraico.
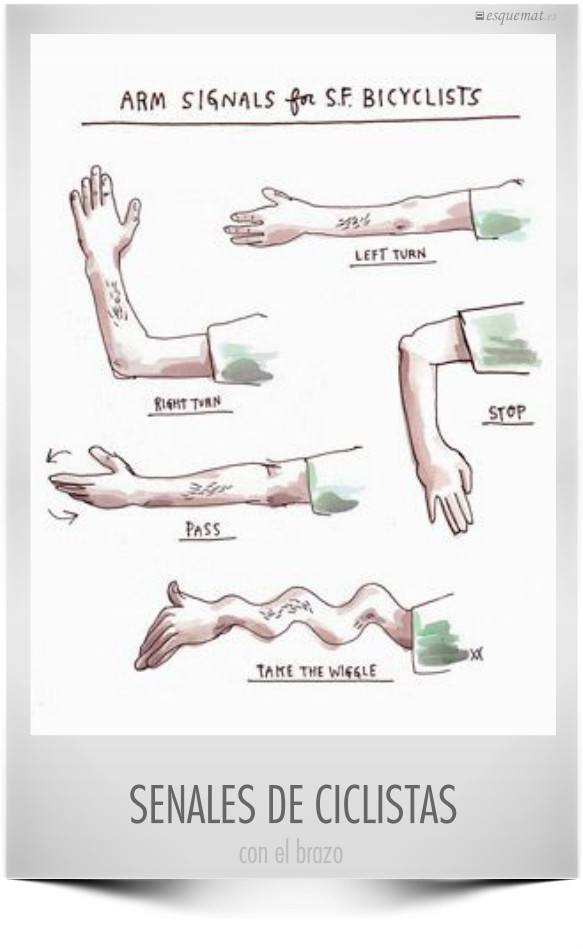
Álgebra de la bicicleta, hecha a mano, los signos que ayudan a circular con seguridad, de la mano de Wendy Macnaughton.
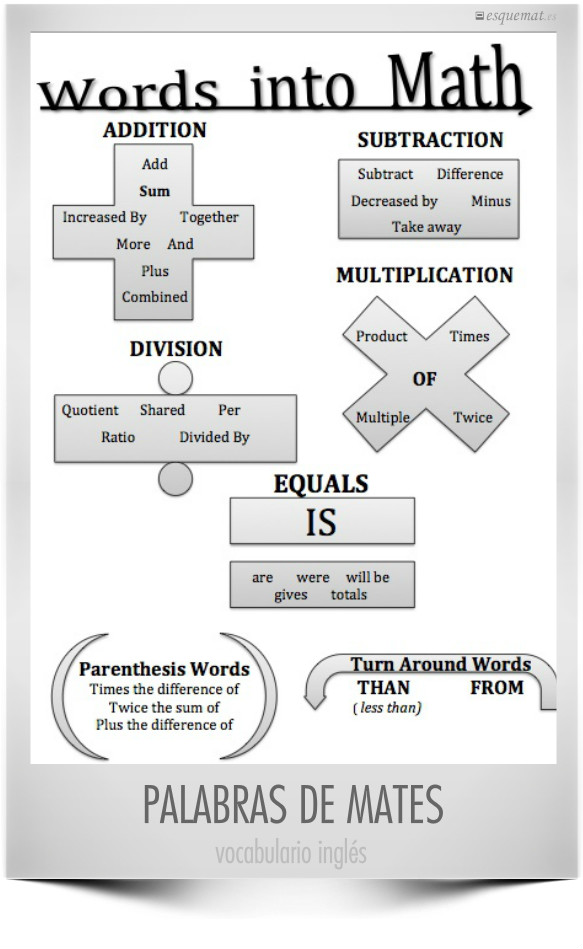
Distintas palabras inglesas relacionadas con operaciones y símbolos matemáticos.
Publicado en ispeakmath.

La idea de esta espiral es simple. Uno empieza con un segmento de longitud 1, añade un ángulo recto con otro lado de longitud 1 y la hipotenusa es igual a raíz de 2. Si se añade un ángulo recto con otro lado de longitud 1, la nueva hipotenusa es raíz de 3. Y repitiendo el procedimiento siempre formando triángulos rectángulos con un lado 1, se obtienen todas las raíces en una hermosa espiral.
Realizado por Feliz Lindemann en TEX y publicado en texample: Rooty helix



