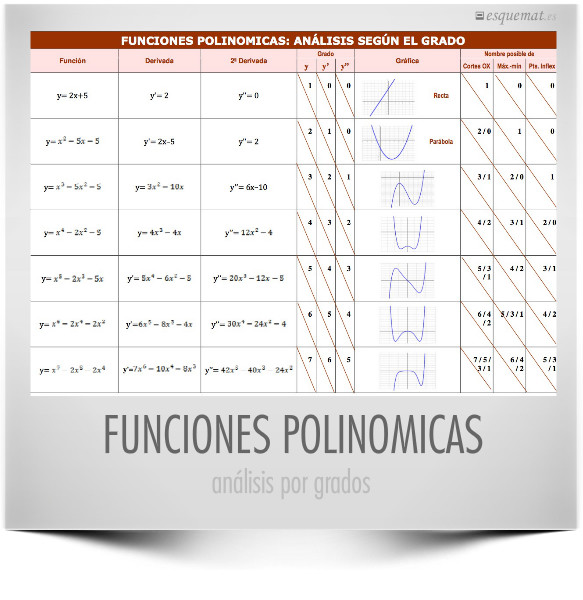
Análisis del comportamiento de las funciones polinómicas según su grado: Se toma una función concreta de 1º, 2º, 3º, 4º… grado, se calcula la 1ª derivada y la 2ª y se comparan sus grados y el número de ceros posibles, según el teorema fundamental del Álgebra (Una ecuación de grado n tiene  n raíces). Luego se mira el número posible de extremos (Max-min) relativos y puntos de inflexión, teniendo en cuenta que sólo sirven las raíces reales y que las complejas, si las hay, van por parejas. Todo ello permite hacer una estimación de la gráfica.

Realizar y observar este trabajo es un buen ejercicio de razonamiento y análisis que ayuda a conocer y dominar los polinomios, sus funciones y gráficas y los conceptos de raíces y puntos singulares.
Esta tabla se desarrolló en clase de 2º de Bach entre el profesor y los alumnos y fue editada posteriormente por el alumno @PepPastor.
Clic en la imagen abre un pdf con el formulario bilingüe en A4.

Esta entrada participa en la edición 3.1415926535 del Carnaval de Matemáticas cuyo blog anfitrión es La Aventura de la Ciencia.